2.1. Operaciones

Termómetro

Imagen en Flickr
de Giulietto86 bajo CC

Los números enteros son una ampliación de los naturales, pues incluyen tanto el cero como los números negativos. Esto implica que se compliquen un poco las propiedades de las operaciones que podemos realizar con ellos.

Al sumar, restar y multiplicar números enteros, el resultado es siempre un número entero. No ocurre lo mismo con la división: al dividir dos números enteros, el resultado es un número entero sólo si el dividendo es múltiplo del divisor.

Por ejemplo: 6/3 sí da un número entero, pero 8/3 ya no es un número entero, sino racional, que los estudiaremos en el siguiente punto del tema. En el caso de 8/3, para números enteros escribimos esa división como: 8 = 2·3 + 2, de forma que el dividendo (D) es igual al divisor (d) por el cociente (c) más el resto (r), dando lugar a la división entera:

 

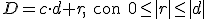
D = c \cdot d + r , \ \begin{verbatim}con\end{verbatim} \ 0\leq\mid{r}\mid\leq\mid{d}\mid\

 

Sumas y restas con enteros. Regla de los signos.

Al hacer sumas y restas con números enteros debes tener en cuenta las dos siguientes reglas de los signos:

a + (-b) = a - b | a - (-b) = a + b

Así tendrías que

4 + (-7) = 4 - 7 = -3

y que 

4 - (-7) = 4 + 7 = 11

A continuación te ofrecemos un vídeo que te permitirán resolver las dudas que puedas tener sobre sumas y restas de enteros.

Vídeo de Tuto mate alojado en Youtube

AV - Actividad de Espacios en Blanco

Día de nieve
Fotografía en Flickr de txindoki bajo CC

Te planteamos el siguiente problema, para practicar las sumas y restas de enteros. El primer día de diciembre de 2009, la temperatura mínima en Granada fue de -1 grados. Completa los espacios blancos que aparecen en la siguiente tabla.

Día Temperatura Diferencia con el día siguiente Operación
1 -1 ºC aumentó en 7 ºC -1 + 7 =
2 ºC disminuyó en 2 ºC
 - 2 = 4
3 4 ºC
 disminuyó en ºC 4 - = -1
4 -1 ºC
 disminuyó en ºC
 - - = -3
5 -3 ºC
 aumentó en 2 ºC
 -3 + =
6 ºC disminuyó en ºC
 - = -4

 

Habilitar JavaScript

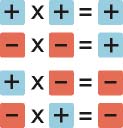
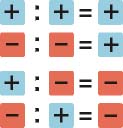
Las reglas de los signos en el producto y la división.

Al multiplicar y dividir números entero

Antonio Ortega Moreno

Tabla de signos
Tabla de signos
Imagen en INTEF de Antonio Ortega Moreno bajo CC

Por ejemplo:

  • 8 · 4 = 32
  • (-8) · (-4) = +32
  • 8 · (-4) = -32
  • (-8) · 4 = - 32
  • 8 : 4 = 2
  • (-8) : (-4) = +2
  • 8 : (-4) = -2
  • (-8) : 4 = -2

 

 

 

 

 

Fíjate que si se omite el signo delante de un número entero, siempre debes entender que es el singo "+".

Propiedades de las operaciones con números enteros.

Sean a, b y c números enteros cualesquiera. Se cumplen las siguientes propiedades:

Propiedades de la suma
Propiedades de la multiplicación
Conmutativa
a+b = b+a
Conmutativa
a · b = b · a
Asociativa
(a+b)+c = a+(b+c)
Asociativa
(a · b) · c = a · (b · c)
Existencia de elemento neutro
a+0 = a
(0 es el elemento neutro de la suma) 		Existencia de elemento neutro
a · 1 = a
(1 es el elemento neutro de la multiplicación)
Existencia de elemento simétrico
a+(-a) = 0
 
Propiedad distributiva de la suma respecto a la multiplicación
(a + b) · c = a · c + b · c

 

 

La propiedad distributiva es muy importante ya que permite sacar factor común cuando un número se repite varias veces:

7·5 + 7·6 - 7·3 = 7 · (5 + 6 - 3) = 7 · 8 = 56

Importante

A la hora de hacer operaciones combinadas, recuerda la prioridad de las operaciones, que es la siguiente, siempre de izquierda a derecha:

  1. Operaciones con paréntesis.
  2. Operaciones con corchetes.
  3. Potencias y raíces (que las estudiarás en este mismo tema).
  4. Multiplicación y división.
  5. Sumas y restas.

Ejemplo o ejercicio resuelto

Realiza las siguientes operaciones combinadas con los números enteros:

5 · 8  -  [-9 - (-4) + (13 - 7)] + 6 + 36 : 9

Por último, en los siguientes vídeos puedes repasar las cuestiones principales que se han visto en este apartado, incluyendo las reglas de los signos y el orden en el que hay que realizar las operaciones.

Vídeo de Tuto mate alojado en Youtube Vídeo de Tuto mate alojado en Youtube