1.1. Números para contar

|
El ser humano ha sentido siempre la necesidad de contar. En un principio, el hombre prehistórico utilizaba piedras y ramas para representar números y operar con ellos. De hecho, la palabra cálculo viene del latín Calculus y significa piedra pequeña o guijarro. Se conoce que la idea de enumerar mediante muescas en un hueso o en la piedra es antiquísima, desde luego anterior a la rueda, aunque posterior a la utilización del fuego.
Los números naturales nos sirven para contar. Si te dicen el número de personas que asisten a un concierto o a una reunión, o te preguntan por la edad, por el número de hijos, o por las estrellas que podrías contar en una noche entera, los estarás usando.
Importante
El conjunto de los números naturales, que lo representaremos por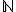 , está formado por los números:
, está formado por los números:
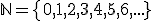
Por tanto, los números naturales son los que empezando en cero (aunque algunos matemáticos proponen que empiezan en el uno), van aumentando de uno en uno, y no tienen final.
Fíjate que, como cualquier conjunto matemático, se expresa poniendo entre llaves unos cuantos de sus elementos. Para expresar que un número pertenece al conjunto de los números naturales, se utiliza el símbolo de pertenencia 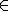 , lo mismo que para indicar, en general, que un elemento forma parte de un conjunto. Por ejemplo, para decir que el 12 es un número natural tendrás que escribir que
, lo mismo que para indicar, en general, que un elemento forma parte de un conjunto. Por ejemplo, para decir que el 12 es un número natural tendrás que escribir que 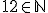 , expresión que se lee "12 pertenece a
, expresión que se lee "12 pertenece a 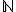 ".
".
Con los números naturales se puede operar, y seguro que recuerdas cómo hacerlo, no obstante el siguiente vídeo nos lo recuerda en un momento:
Importante
En multitud de ocasiones tenemos que realizar más de una operación a la vez. Para ello, tendremos en cuenta la prioridad de las operaciones, que es la siguiente:
- Operaciones con paréntesis y corchetes.
- Multiplicación y división.
- Sumas y restas.
Caso de estudio
En la familia Martínez-Cruz están haciendo un análisis de su economía doméstica. La señora Cruz trabaja por horas con el siguiente horario de trabajo: los lunes, miércoles y viernes trabaja cuatro horas al día, los martes y los jueves sólo tres horas por día y sabemos que cobra a 14 € la hora. Su marido, el señor Martínez tiene un sueldo de 1620 € al mes, y su hijo Miguel gana la mitad que su padre.
¿Cuánto ingresa la familia en dos semanas?
Si la familia destina a pagar la hipoteca la tercera parte de sus ingresos en esos 15 días, a comida 120 € quincenales, a ropa y calzado 250 € mensuales y el resto de gastos aseguran que los cubren con 350 € semanales. ¿Cuánto ahorran cada dos semanas?
Miguel quiere quedarse con la tercera parte de su sueldo para ahorrar y comprarse una moto. ¿Puede asumir la familia esta propuesta sin cambiar el reparto de gastos que tiene?
Pregunta de Elección Múltiple
Pregunta Verdadero-Falso
Retroalimentación
Falso
No hay un número natural que sea el más grande. Pensemos el que pensemos, bastaría con sumarle uno y tendríamos uno mayor. Por cierto, no vale decir infinito, ya que no es un número.
Retroalimentación
Verdadero
Por eso se dice que la suma es una operación interna.
Retroalimentación
Falso
En el conjunto de los números naturales no es posible restar a un número otro que sea mayor. Por este motivo se necesita ampliar los números naturales a un conjunto mayor de números: los números enteros, que estudiarás en el próximo punto del tema.
Por ejemplo, 5 - 8 no es un número natural.
Retroalimentación
Verdadero
Por ejemplo 17 entre 5 no es natural. Para hacer este tipo de divisiones necesitamos los números racionales, que estudiarás en este tema.
Retroalimentación
Verdadero
El orden de los factores no altera el producto y el de los sumandos no altera la suma.