3.5. El campo gravitatorio no se salva
 |
| Imagen en Wikimedia Commons, de Lsmpascal. CC |
Ni el campo gravitatorio ni ningún otro campo de fuerzas se salvan de los efectos de las habilidades de nuestro amigo Gauss, pues su teorema es general para el calculo vectorial. Faltaría menos, toma formas diferentes según a qué tipo de campo vectorial se aplique.
¿Te acuerdas bien del campo gravitatorio? Si aplicas el teorema al mismo, podrías decir que el flujo del mismo a través de una superficie cerrada es proporcional a la masa encerrada por dicha superficie.
Escrito en términos matemáticos, como no podría ser de otra forma, toma la siguiente forma:
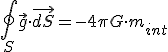
Donde G es la constante de gravitación universal y mint es la masa que queda encerrada dentro de la superficie cerrada S. El resto de magnitudes... no necesitan explicación.
Si aplicas el teorema de Gauss para calcular el campo gravitatorio creado por una esfera en un punto exterior a la misma, podrás comprobar que, en efecto, el campo obtenido es el mismo que el que crearía una masa puntual situada en el centro de la esfera.
 |
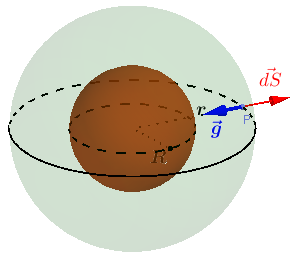| Ilustración en INTEF de Javier López. CC |
El cálculo es fácil. Imagina que tienes un planeta de radio R y masa M. Vas a calcular el campo gravitatorio que crea en el punto P, exterior al planeta. Para ello eliges como superficie gaussiana una esfera de radio r, que contiene al punto P.
Puedes observar que la integral que aparece en el teorema de Gauss es inmediata, dado que en todos los puntos de la esfera de radio r, el campo gravitatorio debe tener el mismo módulo (por la simetría del sistema) y, además, en todos los puntos de la superficie gaussiana, los vectores 
y 
tienen la misma dirección y sentido contrario. Por lo tanto...
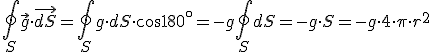
Si aplicas ahora el teorema de Gauss...
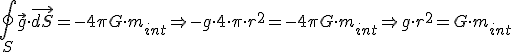
Y si ahora tienes en cuenta que 
(pues el planeta está completamente encerrado en la superficie gaussiana) puedes despejar fácilmente el módulo del campo gravitatorio:
Es por esta razón por lo que en la unidad dedicada al campo gravitatorio podías usar (alegremente) la misma expresión del campo tanto para el creado por una masa puntual como para el creado por un planeta.
Importante
Aplicando el teorema de Gauss a diferentes situaciones en las que se conoce la carga encerrada dentro de una superficie se puede deducir el valor del campo eléctrico.
Objetivos
¿Te has preguntado alguna vez cómo será el campo gravitatorio dentro de un planeta? ¿Seguirá siendo igual al que crearía una masa puntual situada en el centro del planeta?
Si así fuera, ten en cuenta que, justo en el centro del planeta, la intensidad del campo gravitatorio sería infinita ¿no? Puesto que en ese punto r = 0. Esto de los "infinitos" no es algo que nos guste mucho a los físicos... Si te pica la curiosidad, mira qué sucede al aplicar el teorema de Gauss para hacer el cálculo que te comentamos...
Como puedes comprobar, el campo dentro del planeta es muy diferente del que existe fuera. Dentro del planeta el campo no decrece con el cuadrado de la distancia al centro, sino que crece desde su valor mínimo (cero) en el centro del planeta, hasta su valor máximo, en la superficie del mismo.