3.1. Campo eléctrico de una carga puntual

Ilustración en INTEF de Javier López. CC

Puede que aún no te creas que el teorema de Gauss es un herramienta muy útil para calcular campos eléctricos... No te culpo, pues como ya has leído en el apartado 2.3 del tema, el flujo no siempre es fácil de calcular; hacer la integral que aparece en el teorema de Gauss puede tener su complicación.

Pero si se dan las condiciones que se mencionan en ese apartado... la cosa cambia. Para mostrarte la potencia de este teorema, vas a aplicarlo para calcular el campo eléctrico creado por una carga puntual. Recuerda que su expresión ya ha sido establecida en el tema anterior, de manera que podrás comprobar que, en efecto, el teorema de Gauss... ¡Funciona!

El truco está en saber elegir bien la superficie sobre la que tenemos que hacer la integral, la superficie cerrada a través de la cual podamos calcular el flujo de una forma sencilla. A la misma se le conoce como superficie gaussiana.

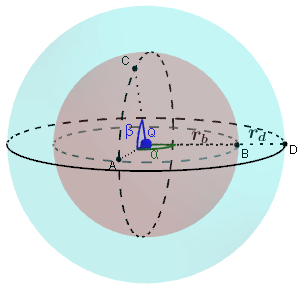
La clave para elegir la superficie gaussiana es la simetría de la distribución de carga. En este caso, como la carga es puntual, la simetría del campo creado por ella debe ser esférica ¿Y qué significa esto de la simetría? Observa la imagen de la derecha y lo comprenderás.

Imagina que en el Universo solo estáis la carga puntual y tú. Tú estás mirando fijamente a la carga... ¿Serías capaz de distinguir si la estás mirando desde el punto A o desde el punto B? La respuesta está clara: No. Tampoco podrías distinguir si la miras desde el punto A o el C. Sin embargo, sí podrías distinguir si la estás mirando desde cualquiera de ellos (A, B, C) o desde el punto D.

Esto es la simetría, esférica en este caso. La carga "se ve" del mismo modo siempre que la mires desde la misma distancia. Todos los puntos "indistinguibles" de antes (A, B, C) están a la misma distancia de la carga (r_b). No así el punto D, que está más lejos y eso... sí lo notarías.

La información que nos ofrece la simetría es vital para lo que se pretende hacer. En este caso, la simetría te está diciendo que el módulo el campo eléctrico creado por la carga no depende de los ángulos α o β, sino tan solo de la distancia a la carga, r. Por lo tanto, dada una esfera centrada en la carga, el campo eléctrico tendrá el mismo módulo en todos los puntos de la misma.

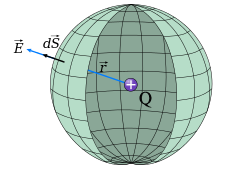
¿Y qué dirección y sentido deberá tener el campo? También la simetría permite pensar que la dirección debe ser radial. El sentido vendrá dado por el signo de la carga; si ésta es positiva el sentido será hacia afuera, como en la imagen de la izquierda, y si es negativa será hacia dentro. 

Adaptado de ilustración en Wikimedia Commons de Chanchocan . CC

Todas estas consideraciones de simetría (que son más fáciles de entender que de contar) simplifican enormemente los cálculos. La integral se convierte en casi inmediata. ¡Incluso sin saber cuánto vale el campo!... Solo sabiendo la "pinta" que debe tener:

En primer lugar, en todos los puntos de S, y  son paralelos; forman un ángulo de 0º. Por lo tanto...

 

En segundo lugar, E toma el mismo valor en todos los puntos de S; es constante, lo que te permite "sacarlo" de la integral:

 

Por último, la integral anterior no es sino el área de la superficie gaussiana

 

Y como esta superficie es una esfera de radio r, cuya área es 4πr², ya tienes el fluyo calculado:

  

Como ves, no ha sido difícil calcular el flujo ¿verdad? Ahora es cuando entra en acción el teorema de Gauss, según el cual: . De manera que, como la carga interior es justo el valor de la carga puntual, puedes escribir...

 

Y de aquí despejar el módulo del campo eléctrico:

¿Es o no es la expresión que ya conocías para el campo eléctrico creado por una carga puntual?... ¡Funciona!