2. Probabilidad: Teoría y problemas

1. Primeros pasos

Espacio muestral

Definición.- El espacio muestral E asociado a un experimento aleatorio es el conjunto de resultados elementales que pueden obtenerse en dicho experimento. El conjunto formado por uno o varios resultados elementales recibe el nombre de Suceso. Como conjuntos que son los sucesos, podemos efectuar las mismas operaciones entre ellos, como por ejemplo, la unión, la intersección y el suceso complementario.

Ideas previas: Ya debemos saber de situaciones de aprendizaje anteriores, cómo conseguir los conjuntos unión, intersección y contrario, no obstante vamos a recordarlos brevemente:

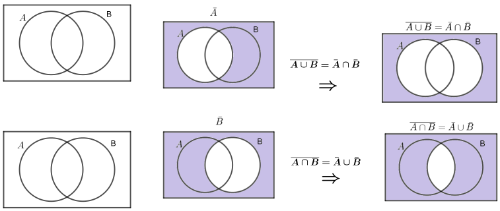
  • Conjunto unión: Se representa por $A\cup B $ y está formado por los elementos que pertenecen a A o a B, lógicamente sin repetirlos, si un elemento pertenece al mismo tiempo a A y a B solo se pone una vez en el conjunto unión.
  • Conjunto intersección: Se representa por $A\cap B $ y está formado por los elementos que pertenecen a A y a B al mismo tiempo, es decir sólo contiene los elementos que pertenecen a los dos conjuntos simultáneamente.
  • Conjunto contrario: Se representa habitualmente como  $\bar A $, aunque puede encontrarse en otros libros o tratados de otras dos formas: $A'$ o $A^{C}$ y está formado por el resto de elementos del espacio muestral que no pertenecen a A.

Ejemplo. El espacio muestral asociado a un experimento aleatorio es E = {a, b, c, d, e, f, g}. Se definen los sucesos A, B y C de la siguiente manera:

 A = {a, b, c}   B = {b, e, f, g}  C = {a, b, e, g}.

Si notamos por $\cup, \cap,$ a la unión e intersección de sucesos y al suceso complementario de A, lo notamos por $\bar{A};$  averigua la composición de los siguientes sucesos:

a) $A\cup B $
b) $A\cap C $
c) $A\cap B\cap C $
d) $\bar A\cup C $
e) $\bar B\cap\bar C $
f) $\bar A\cup \bar C $

g

Solución:

E = {a, b, c, d, e, f, g}; 
A = {a, b, c}   B = {b, e, f, g}  C = {a, b, e, g}.

a) $A\cup B $={a, b, c, e, f, g}
b) $A\cap C $={a, b}
c) $A\cap B\cap C $={b}
d) $\bar A\cup C $={a, b, d, e, f, g}
e) $\bar B\cap\bar C $={c, d}
f) $\bar A\cup \bar C $={c, d, e, f, g}

Probabilidad - Frecuencia relativa

Ideas previas: Como ya hemos visto en los apartados anteriores, todos tenemos una intuición probabilística que nos indica con mucha frecuencia la probabilidad correcta, sin embargo, no siempre es tan sencillo. La regla de Laplace  nos indica que en el caso en que todos los sucesos elementales tengan la misma probabilidad, podemos calcular la probabilidad de un suceso dividiendo el número de casos favorables entre el número de casos posibles, por eso cuando en una bolsa opaca tenemos dos bolas rojas y tres blancas que sean del mismo tamaño y características, podremos calcular la probabilidad de sacar una bola blanca o roja dividiendo el número de casos favorables entre el número de casos posibles, así podemos concluir:

$P(R)={\Large{\frac{2}{5}}}$

$P(B)={\Large{\frac{3}{5}}}$

Regla de Laplace: $P(A)={\Large{\frac{\text{Nº de casos favorables}}{\text{Nº de casos posibles}}}}$

Pero ojo que esto no ocurre siempre, como veremos en el ejemplo siguiente, es condición indispensable para poder aplicar la regla de Laplace que las probabilidades de los sucesos elementales sea la misma y esto no ocurre siempre.

Ejemplo. Se lanzan dos dados y anotamos los puntos de las caras superiores. Sean los sucesos A = {la suma de las puntuaciones es 5} y B = {las dos puntuaciones son números primos}. Halla las probabilidades de los siguientes sucesos:

a) $A$
b) $B$
c) $A\cup B$
d) $A\cap B$

Solución:

Si en este problema buscamos el espacio muestral, es decir los resultados posibles, encontraremos que el menor valor que podemos obtener es el 2, sacando un uno en cada dado y el máximo 12 sacando un seis en cada dado. Por tanto el espacio muestral del experimento sería: 

$E=\{2,3,4,5,6,7,8,9,10,11,12\}$

Podemos fijarnos en estos valores y vemos que hay más números pares que impares, y concluir erróneamente que la probabilidad de obtener un número par es mayor que la de obtener un número impar, hay once posibles resultados y seis son pares, podríamos decir que la probabilidad de sacar par sea:

 $P(P)={\Large{\frac{\text{Nº de casos favorables}}{\text{Nº de casos posibles}}}}={\Large{\frac{6}{11}}}$

¡Pero esto es un error! ¿Por qué?

Porque esos sucesos no son equiprobables.

Para obtener sucesos elementales equiprobalbes, tenemos que descender en la estructura del problema, si consideramos todos los valores posibles de cada dado y los asociamos dos a dos, entonces todas las probabilidades si que serán la misma, cada pareja de valores tiene una probabilidad de salir de un caso de 36 posibles (seis por seis), pero muchos de esos casos aportan el mismo valor como suma de sus caras, por ejemplo, sacar dos solo se puede obtener sacando un uno en cada dado, con el par (1,1), sin embargo sacar siete como suma de los dados puede obtenerse con muchas parejas, en concreto con todas estas: 

(1,6); (2,5); (3,4); (4,3); (5,2); (6,1)

Lo que significa que sacar un 7 como suma de los dados es seis veces más probable que sacar un 2.

Por todo esto y teniendo en cuenta que todos los resultados son ahora equiprobables, es decir, tienen la misma posibilidad de salir, cuando los consideramos como parejas de dos dados (a,b), con a y b entre 1 y 6 y que el orden en los resultados implican sucesos distintos,  (1,4) y (4,1) son sucesos distintos entre sí. Estaremos de acuerdo que en total habrá $6·6=36$ resultados posibles. Por tanto, la probabilidad en este experimento la podemos calcular como el cociente entre el número de Casos Favorables y el número total de Casos Posibles. A esta ley la conocemos con Regla de Laplace, en honor a su autor.

Pierre-Simon Laplace
Imagen de Jimmy44 en Wikimedia Commons.. Pierre-Simon Laplace (CC0)




En cada apartado pedido damos dos pasos, primero detectar las parejas que son favorables al ejercicio y luego aplicar la regla de Laplace:

a) $A$={(1,4),(2,3),(3,2),(4,1)} $ \rightarrow P(A)={\Large{\frac{4}{36}}}={\Large{\frac{1}{9}}}$

b) $B$={(1,1),(1,2),(1,3),(1,5),(2,1),(2,2),(2,3),(2,5),(3,1),(3,2),(3,3),(3,5),(5,1),(5,2),(5,3),(5,5)} $ \rightarrow P(B)={\Large{\frac{16}{36}}}={\Large{\frac{4}{9}}}$

c) $A\cup B$={(1,1),(1,2),(1,3),(1,4),(1,5),(2,1),(2,2),(2,3),(2,5),(3,1),(3,2),(3,3),(3,5),(4,1),(5,1),(5,2),(5,3),(5,5)} $ \rightarrow P(A\cup B)={\Large{\frac{18}{36}}}={\Large{\frac{1}{2}}}$

d) $A\cap B$={(2,3),(3,2)} $ \rightarrow P(A\cap B)={\Large{\frac{2}{36}}}={\Large{\frac{1}{18}}}$

Técnicas de recuento

Ideas previas: Todo lo necesario para este apartado ya lo hemos estudiado en la primera situación de aprendizaje del curso, "Más coches que matrículas" donde se hizo un estudio concienzudo sobre las técnicas de recuento. Estas técnicas son muy importantes para determinar tanto los casos favorables como los casos posibles de un problema de probabilidad, cuantificar esos dos valores nos llevará a resolver el problema con una simple división. Por este motivo esas técnicas son tan importantes en probabilidad.

Ejemplo. Javier ha encontrado cuatro huevos de pavo real. Cree que lo más probable es que sean dos machos y dos hembras, ya que la probabilidad de ser macho o hembra es la misma. ¿Es cierto o se equivoca?

Solución:

Notamos por H y M, a los huevos que dan lugar a Hembra y Macho, respectivamente. Por tanto, 4 huevos pueden dar lugar a los siguientes resultados:

  • Los casos en los que los 4 huevos tienen el mismo sexo son únicos: HHHH o MMMM, se trata de una combinación de cuatro elementos tomados de cuatro en cuatro, o de cero en cero, según a quién consideremos: En cada caso tendremos:

$\left (\begin {array} {c} 4 \\ 0\end {array} \right)=\left (\begin {array} {c} 4 \\ 4\end {array} \right)={\Large{\frac{4!}{4! · 0!}}}=1$

  • Los casos que tienen un huevo de un sexo y tres del otro son los siguientes, recordad que simplemente debemos ir desplazando el lugar ocupado por el huevo de diferente sexo al lugar adyacente hasta llegar desde el primer lugar al último, consideramos aquí ambos casos uno M con tres H o uno H con tres M:

HMMM
MHMM
MMHM
MMMH

MHHH
HMHH
HHMH
HHHM

En cualquier caso, el recuento nos lo dan las combinaciones de cuatro elementos tomados de tres en tres o de uno en uno:

$\left (\begin {array} {c} 4 \\ 3\end {array} \right)=\left (\begin {array} {c} 4 \\ 1\end {array} \right)={\Large{\frac{4!}{1! · 3!}}}=4$

  • Los casos que tienen dos huevos de cada sexo los podemos poner de entrada separados dos a la derecha y dos a la izquierda e ir desplazando hacia el otro lado de uno en uno hasta llegar al final:

HHMM
HMHM
HMMH
MHHM
MHMH
MMHH

En este caso se trata de combinaciones de cuatro elementos tomados de dos en dos, con lo que el recuento sería:

$\left (\begin {array} {c} 4 \\ 2\end {array} \right)={\Large{\frac{4!}{2! · 2!}}}={\Large{\frac{4·3·2·1}{2·1 · 2·1!}}}=3·2=6$


Como vemos, hay 6 casos en los que la familia tiene 2 hembras y 2 machos. La probabilidad por tanto será igual a:

$P_1={\Large{\frac{6}{16}}}={\Large{\frac{3}{8}}}$.

Sin embargo hay 8 casos en los que hay 3 pavos de un sexo y 1 del otro. Esta posibilidad, por tanto, será más factible, siendo su probabilidad:

$P_2={\Large{\frac{8}{16}}}={\Large{\frac{1}{2}}}$.

Diagramas de árbol

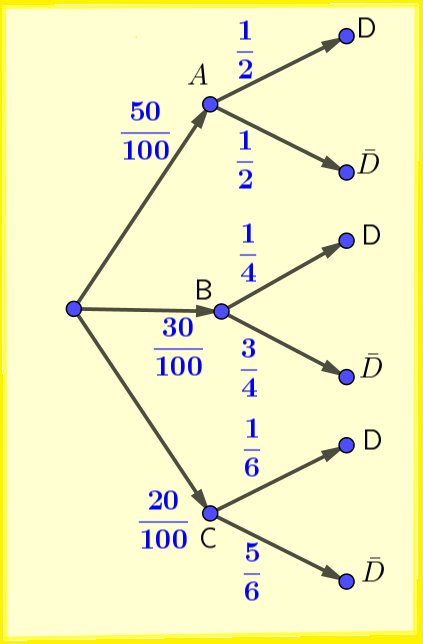
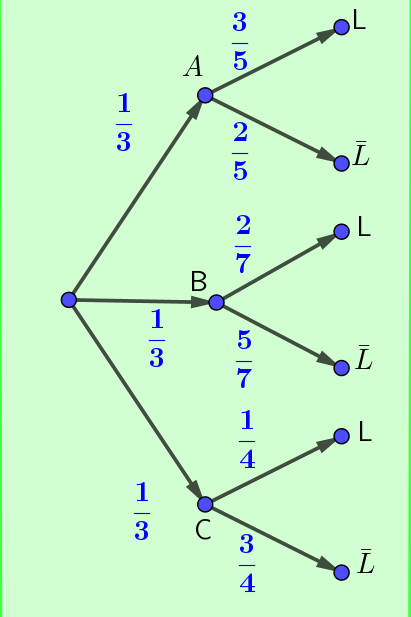
Ideas previas: Un diagrama de árbol, es una técnica de representación gráfica de un problema que puede tener diferentes opciones. Es la representación de los posibles resultados de un experimento que consta de diversos pasos. En un diagrama de árbol realizamos primero un experimento aleatorio y representamos sus finitas posibilidades partiendo de un mismo nodo que por medio de una linea nos lleva a cada una de estas posibilidades, en dichas lineas colocamos la probabilidad de cada posibilidad. Después, de cada uno de los resultados posibles salen diferentes lineas que representan un segundo experimento, igualmente con sus probabilidades sobre la linea. De esta forma tenemos una visual gráfica y completa de todas las probabilidades, donde es muy importante, que la suma de todas las probabilidades que salen de un mismo nodo sea 1. Lo veremos en el siguiente ejemplo concreto.

Ejemplo: En un concurso hay dos bolsas. En la bolsa A hay 3 bolas verdes y 2 rojas y en la bolsa B hay 7 bolas verdes, 3 bolas negras y 5 bolas rojas. Tienes que elegir una bolsa y sacar una bola roja para ganar un premio. Expresa el problema por medio de un diagrama de árbol y cuantifica cada una de las probabilidades implicadas en el árbol.

Solución:

Diagrama de árbol
Imagen de elaboración propia. Diagrama de árbol (CC BY-NC-SA)
 


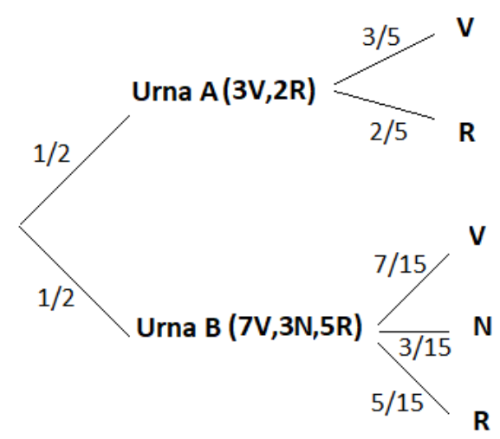
En este caso la interpretación del problema es sencilla, primero elegimos una de las dos urnas que consideramos iguales y esa elección tendrá una probabilidad igual para ambos casos, por eso en las primeras líneas que llevan a Urna A y Urna B ponemos una probabilidad de $\Large{\frac{1}{2}}$, mientras que en las líneas que salen de cada urna y llevan a los colores que podemos obtener de las bolas extraídas,  los valores de la probabilidad están afectados por el contenido de cada urna. La lógica y nuestra intuición probabilística mencionada en el apartado anterior nos indica acertadamente que debemos aplicar la regla de Laplace dado que la probabilidad de elegir una bola concreta de entre todas es la misma para cualquier bola, por eso en la primera urna que hay tres bolas verdes y dos rojas, las probabilidades respectivas de sacar una bola de color roja es $\Large{\frac{3}{5}}$ y la de sacar una bola verde $\Large{\frac{2}{5}}$, en cada caso el cociente de los casos favorables entre los casos posibles. Finalmente rellenamos también las probabilidades de las bolas de la segunda urna, donde hay 15 bolas en total con la distribución de siete verdes, tres negras y cinco rojas, y por tanto las probabilidades, aplicando de nuevo la regla de Laplace, son respectivamente: $\Large{\frac{7}{15}}$; $\Large{\frac{3}{15}}$ y $\Large{\frac{5}{15}}$

Puede comprobarse fácilmente que la suma de todas las probabilidades que salen de cualquiera de los nodos es uno:

${\Large{\frac{1}{2}}}+{\Large{\frac{1}{2}}}={\Large{\frac{1+1}{2}}}=1$

${\Large{\frac{3}{5}}}+{\Large{\frac{2}{5}}}={\Large{\frac{3+2}{5}}}=1$

${\Large{\frac{7}{15}}}+{\Large{\frac{3}{15}}}+{\Large{\frac{5}{15}}}={\Large{\frac{7+3+5}{15}}}=1$

Tablas de contingencia

Ideas previas: Las tablas de contingencia ya las hemos estudiado en la situación de aprendizaje número dos de este tercer bloque "¿Causalidad o casualidad?" y aunque allí las tratábamos como variables estadísticas, podemos entenderlas aquí asociando la frecuencia relativa a la probabilidad de cada supuesto. En este caso el problema consiste en asignar las entradas horizontales a las posibilidades de uno de los experimentos y las verticales al otro, son muy comunes en los casos de que cada experimento tenga dos posibilidades como en el ejemplo que se describe a continuación. En este caso no hay un experimento que siga al otro como en el caso del diagrama de árbol que si tiene una secuencia lógica, primero elegimos una urna y luego sacamos una bola, en estos casos podremos entrar primero por la horizontal o por la vertical. La tabla se construye escribiendo en su interior todas las probabilidades, donde cada celda nos indica de que probabilidad se trata, de manera que si nuestro caso tuviera dos posibles variables $A$ y $B$ por ejemplo, con dos valores cada una $A \text{ y } \bar A$ y $B \text{ y } \bar B$, la tabla requeriría introducir las siguientes probabilidades:

$B$ $\bar{B}$ TOTALES
$A$ $P \left( A \cap B \right)$ $P \left( A \cap \bar{B} \right)$ $P \left( A \right)$
$\bar{A}$ $P \left( \bar{A} \cap B \right)$ $P \left( \bar{A} \cap \bar{B} \right)$ $P \left( \bar{A} \right)$
TOTALES $P \left( B \right)$ $P \left( \bar{B} \right)$ 1

Ejemplo. Se sabe que el 80% de los visitantes de un determinado museo son andaluces y que el 55% son andaluces y adultos. Además, el 17% de los visitantes no son andaluces pero si adultos. Se elige, al azar, un visitante del museo. Realiza una tabla de contingencia para determinar cada una de las probabilidades.

Solución:
Realizamos la tabla de contingencia:

$A$=Andaluz $\bar{A}$= No Andaluz TOTALES
$D$=Adulto 0.55 0.17 0.72
$\bar{D}$= No Adulto 0.25 0.03 0.28
TOTALES 0.8 0.20 1

El proceso para rellenar esta tabla es el siguiente: primero colocamos las probabilidades dadas por el enunciado, son las escritas en color negro, el total de andaluces es el 80% y por tanto es 0.8; la intersección de andaluces y adultos es del 0.55 (55%) y la celda confluencia de no andaluz y adulto es 0.17 (17%), Estos son los datos del problema a los que añadimos uno que es evidente y siempre debe cumplirse, la confluencia de totales y totales debe ser la unidad, es 1 porque lo engloba a todo. Bien pues los datos que están en rojo se calculan simplemente por diferencia y suma:

  • El total de adultos debe ser la suma de las dos celdas de la izquierda, $0.55+0.17=0.72$
  • El total de no adultos será la diferencia entre 1 y el valor calculado anteriormente: $1-0.72=0.28$
  • La confluencia de No adulto y Andaluz debe ser la diferencia entre el total andaluz y andaluz adulto: $0.8-0.55=0.25$
  • El total de no andaluz se obtiene por diferencia entre el total-total y el total Andaluz: $1-0.8=0.20$
  • Y finalmente la confluencia entre No andaluz y No adulto podemos hacerlo de dos formas y comprobar que sale lo mismo, podemos restar al total No andaluz el adulto no andaluz: $0.20-0.17=0.03$ que sale lo mismo que restar al total No adulto el andaluz no adulto: $0.28-0.25=0.03$

2. Teoría de la probabilidad

1. Definición de un modelo de probabilidad

Un modelo de probabilidad es una función $P$, que a cada suceso $A$ le hace corresponder un número $P(A)$ entre 0  y 1, verificando:

a) $P(E)=1$, siendo $E$ el espacio muestral (=Conjunto de todos los sucesos).

b) Si $A_1,A_2,...,A_n$ son sucesos disjuntos o incompatibles ($A_i∩A_j=∅$), entonces: $P(∪_nA_n)=∑_nP(A_n)$.

La definición no resuelve el problema de asignar probabilidades a diferentes sucesos, pero sí impone ciertas condiciones de coherencia para cualquier modelo de probabilidad. 

2. Propiedades de un modelo de probabilidad

A partir de estas exigencias se pueden obtener las siguientes propiedades que son sencillas de probar:

  1. Para cualquier suceso $A$, $P(\bar{A})=1-P(A)$, donde $P(\bar{A})$ es el suceso complementario de A en E.

  2. $P(∅)=0$, donde $∅$ es el suceso vacío.

  3. $A⊂B⇒P(A)≤P(B)\ y\ P(B-A)=P(B)-P(A)$

  4. $P(A∪B)=P(A)+P(B)-P(A∩B)$

  5. $P(\cup _{i=1}^nA_i)=\sum _{i=1}^n P(A_i)-\sum _{i<j}^n P(A_i\cap A_j)+...+(-1)^{k+1}\sum _{i_1<i_2<...<i_k}^n P(A_{i_1}\cap A_{i_2}\cap ...\cap A_{i_k})+...$

3. Espacios muestrales discretos 

Una buena parte de los experimentos aleatorios que vamos a considerar son especialmente sencillos de describir ya que constan solamente de un conjunto finito de posibles resultados. Esto significa que el espacio muestral E admite una descripción de la forma:
$E=\left\{a_1,a_2,\text{...},a_n\right\}$. Cuando el espacio muestral es discreto, el modelo de probabilidad queda perfectamente especificado dando la probabilidad de cada suceso elemental, es decir, sólo tendríamos que dar los valores $P(a_i),...,P(a_n)$, verificando:

i) $P(a_k)≥0, ∀a_k$

ii) $∑_{k=1}^nP(a_k)=1$

Resulta evidente, en este tipo de modelos, que para cualquier suceso B, formado por la unión de un número de sucesos elementales $a_i$ del espacio E, se verifica:

$P(B)=∑_{i=1}^lP(a_i)$. 

4. Espacio muestral con sucesos equiprobables: Regla de Laplace

Una situación que frecuentemente sucede en un espacio muestral finito es que todos los sucesos sean igualmente probables. Esto significa que para $E=\left\{a_1,a_2,\text{...},a_n\right\}$ obtenemos que $P(a_1)=P(a_2)=...=P(a_n)={\Large{\frac{1}{n}}}$ y entonces, en este caso, para cualquier suceso $B=\left\{a_1,a_2,\text{...},a_k\right\}$, obtendríamos la muy popular Regla de Laplace, conocida por el nombre de su creador Pierre Simon Laplace (1749 - 1827),

$P(B)=∑_{i=1}^kP(b_i)={\Large{\frac{k}{n}}}={\Large{\frac{Casos\ favorables}{Casos\ posibles}}}$.

5. Álgebra de Boole de sucesos

Consideremos un experimento aleatorio. Dicho experimento tendrá asociado un espacio muestral E. Consideremos también en dicho espacio muestral el conjunto de todos los sucesos posibles de dicho experimento al que normalmente se le nota con la letra griega omega, Ω.  El conjunto de todos los sucesos de un espacio muestral, junto con las operaciones unión (∪) e intersección (∩), cumple una serie de propiedades que lo dotan de una estructura matemática conocida como Álgebra de Boole. En la siguiente tabla se resumen las propiedades y consecuencias directas más importantes que se desprenden de dicha estructura:

Propiedades ∪= Unión ∩= Intersección
Asociativa $A∪(B∪C)=(A∪B)∪C$ $A∩(B∩C)=(A∩B)∩C$
Conmutativa $A∪B=B∪A$ $A∩B=B∩A$
Idempotente $A∪A=A$ $A∩A=A$
Distributiva $A∪(B∩C)=(A∪B)∩(A∪C)$ $A∩(B∪C)=(A∩B)∪(A∩C)$
Complementario $A∪\bar{A}=E$ $A∩\bar{A}=∅$

Unas consecuencias importantes que se deducen de estas propiedades son las leyes de De Morgan, que son muy útiles en la práctica, ya que en muchas situaciones se podrán calcular probabilidades de un suceso a partir de las probabilidades de otros más fáciles o bien que se den como datos.
Son estas dos, las leyes De Morgan:

$\overline{A\cup B}=\bar{A}\cap \bar{B};\ \overline{A\cap B}=\bar{A}\cup \bar{B}$

Leyes De Morgan.
Imagen de elaboración propia. Leyes De Morgan. (CC BY-NC-SA)

6. Probabilidad condicionada

La probabilidad de un suceso depende de la mayor o menor información que tengamos. El concepto de probabilidad condicionada va ligado siempre a sucesos compuestos, en el sentido de que la ocurrencia o no de uno de ellos influya o no en la ocurrencia o no del otro. Siempre que tenga sentido, se denomina probabilidad condicionada del suceso 𝐴 respecto del suceso 𝐵, (probabilidad de 𝐴 condicionado a 𝐵) y se representa P(𝐴/𝐵) al cociente:

$P(A/B)={\Large{\frac{P(A∩B)}{P(B)}}}$, siempre que $P(B) \neq 0$. 

De esta definición se obtiene la fórmula general para la probabilidad de la intersección de sucesos. Se trata de la igualdad P(𝐴∩𝐵)=P(𝐴)⋅P(𝐵/𝐴). Esta fórmula se puede generalizar para un número cualquiera de sucesos:

$P(𝐴_1∩𝐴_2∩𝐴_3⋯∩𝐴_𝑛)=P(𝐴_1)⋅P(𝐴_2/𝐴_1)⋅P(𝐴_3/𝐴_1∩𝐴_2)⋯P(𝐴_𝑛/𝐴_1∩⋯∩𝐴_{𝑛−1})$.

7. Sucesos independientes

Resulta fácil interpretar que dos sucesos sean independientes cuando la ocurrencia de uno no influya en la ocurrencia del otro. Sin embargo, a veces este grado de influencia no resulta fácil de apreciar. Formalizaremos por ello este concepto. Dos sucesos $A$ y $B$ son independientes cuando $P(A∩B)=P(A)·P(B)$. La siguiente propiedad pone de relieve el significado intuitivo de la definición de independencia diciendo que dos sucesos $A$ y $B$ son independientes es equivalente a decir que $P(A/B)=P(A)$.

En efecto, si $A$ y $B$ son independientes, podemos entonces expresar:

$P(A/B)={\Large{\frac{P(A∩B)}{P(B)}}}={\Large{\frac{P(A)·P(B)}{P(B)}}}=P(A)$.

Recíprocamente, si  $P(A/B)=P(A)$, tenemos que:

$P(A)=P(A/B)={\Large{\frac{P(A∩B)}{P(B)}}}⇒P(A∩B)=P(A)·P(B)$.

Esta fórmula se conoce con el nombre de criterio de independencia y es lo que en la práctica nos lleva a calificar sucesos como independientes.

8. Reglas útiles para el cálculo de probabilidades

Observaremos finalmente tres reglas cuyo objetivo es el de facilitarnos el cálculo de probabilidades en distintas situaciones:

  1. REGLA DE LA MULTIPLICACION.

    $P(𝐴_1∩𝐴_2∩𝐴_3⋯∩𝐴_𝑛)=P(𝐴_1)⋅P(𝐴_2/𝐴_1)⋅P(𝐴_3/𝐴_1∩𝐴_2)⋯P(𝐴_𝑛/𝐴_1∩⋯∩𝐴_{𝑛−1})$.

    Esta regla será útil cuando queramos hallar la probabilidad de ocurrencia simultánea de varios sucesos y las probabilidades condicionadas del segundo miembro sean sencillas de calcular. Naturalmente, en el caso de que los sucesos sean independientes, tenemos:

    $P(𝐴_1∩𝐴_2∩𝐴_3⋯∩𝐴_𝑛)=P(𝐴_1)⋅P(𝐴_2)⋅P(𝐴_3)⋯P(𝐴_𝑛)$.

  2. REGLA DE LA PROBABILIDAD TOTAL.

    Sean $A_1,A_2,...,A_n$ sucesos tales que se verifica:

    i) $A_1∪A_2∪...∪A_n=E$.

    ii) $A_i∩A_j≠∅$, para todo $i≠j$.

    Entonces $P(B)=\sum_{i=1}^{n}{P(A_i)·P(B/A_i)}$.

  3. REGLA DE BAYES.

    Sean $A_1,A_2,...,A_n$ sucesos tales que se verifica:

    i) $A_1∪A_2∪...∪A_n=E$.

    ii) $A_i∩A_j≠∅$, para todo $i≠j$.

    Entonces $P(A_j/B)={\Large{\frac{P(A_j∩B)}{P(B)}}}={\Large{\frac{P(A_j)·P(B/A_j)}{P(B)}}}$ y, consecuentemente:

    $P(A_j/B)={\Large{\frac{P(A_j)·P(B/A_j)}{\sum_{i=1}^{n}{P(A_i)·P(B/A_i)}}}}$

La regla de probabilidad total y la regla de Bayes van a ser especialmente útiles cuando se den las siguientes circunstancias:

  1. El experimento aleatorio se puede separar en dos etapas.
  2. Es sencillo dar una partición de todo el espacio muestral $E$ mediante sucesos $A_1,A_2,...,A_n$ correspondientes a resultados de la primera etapa del experimento.
  3. Son conocidas las probabilidades $P(A_1),P(A_2),...,P(A_n)$.
  4. Son fácilmente calculables las probabilidades $P(B/A_1),P(B/A_2),...,P(B/A_n)$.

Cuando se dan estas circunstancias, la regla de la probabilidad total será muy útil para calcular $P(B)$, y la regla de Bayes será muy conveniente para obtener $P(A_j/B)$.

Lanzamiento de dos dados.
Imagen de elaboración propia generada con Bing Creator. Lanzamiento de dos dados. (CC0)

3. Comprueba lo que sabes: Alea iacta est

Después de iniciarte en los conceptos teóricos básicos del Cálculo de Probabilidades has alcanzado el nivel suficiente para aplicarlos y así reforzar tu comprensión. Con una base sólida en este inicio, te estarías preparando para abordar desafíos más avanzados y perfeccionar tus habilidades en la Resolución de Problemas. Con este conjunto de Actividades es muy probable que aprendas mucho sobre el azar.

Elige entre los ejercicios que te presentamos a continuación, y comienza a aplicar tus conocimientos.

Opción A: Completa los huecos

Lee el párrafo que aparece abajo y completa las palabras que faltan:

no se obtienen/ Suceso seguro/ no tiene ningún elemento/ aleatorio/ elemental/ espacio muestral/ ∅/
/se obtienen/ incompatibles/ lanzamos una moneda/ todos los sucesos elementales/ Suceso/ no se verifica A

CONCEPTOS BÁSICOS (I)
Vamos a recordar una serie de conceptos para poder consolidarlos.

  • Fenómeno determinístico.- Cuando al repetirlo bajo idénticas condiciones iniciales siempre los mismos resultados.
  • Fenómeno aleatorio.- Cuando al repetirlo bajo idénticas condiciones iniciales siempre los mismos resultados. Ejemplo: cuando al aire observando la sucesión de caras y cruces que presentan.
  • Experimento .- Operación que repetimos bajo idénticas condiciones iniciales y no se obtienen siempre los mismos resultados.
  • Suceso .- Cada uno de los resultados posibles del experimento aleatorio; luego un suceso elemental consta de un solo elemento del .
  • Espacio muestral.- Conjunto de del experimento aleatorio y lo designaremos como E.
  • .- Conjunto formado por uno o más sucesos elementales, es decir, un subconjunto de resultados elementales del experimento aleatorio.
  • .- Coincide con todo el espacio muestral, ya que al realizar el experimento aleatorio se obtendrá con seguridad uno de los posibles resultados o sucesos elementales, y por tanto ocurrirá E.
  • Suceso imposible.- Es el que del espacio muestral E, y por tanto no ocurrirá nunca, y se representa como . Ejemplo: En el lanzamiento del dado no puede darse el 7.
  • Suceso complementario a un suceso A: Es el suceso que se verifica si, como resultado del experimento aleatorio, . Se acostumbra a denotar con el símbolo Ā.
  • Sucesos : Los sucesos A y B son mutuamente excluyentes si no pueden ocurrir a la misma vez. 

CONCEPTOS BÁSICOS (II)
Coloca al lado la letra V o F según consideres que la proposición es verdadera o falsa, respectivamente.

  1. Un suceso es un subconjunto del espacio muestral que contiene sólo un resultado del experimento aleatorio.
  2. Uno de los axiomas establece que la suma de las probabilidades de un suceso y su complementario es igual a uno.
  3. Uno de los axiomas de la probabilidad establece que la probabilidad del evento vacío es igual a cero.
  4. El número de elementos de un conjunto determina su cardinalidad.
  5. Todos los resultados de un experimento aleatorio son equiprobables.
  6. Si dos eventos no vacíos son independientes, entonces la probabilidad de la unión de ellos es la suma de sus probabilidades.
  7. Si A y B son eventos independientes no vacíos, entonces los eventos complementarios A y B también lo son.
  8. De una caja con X pelotas blancas e Y pelotas rojas se realiza una extracción de 3 pelotas con reposición. La probabilidad de obtener tres pelotas blancas es X3/(X + Y)3.

Habilitar JavaScript

Opción B: ¿Sabemos contar?

Pregunta

Ejercicio 1.- En un colegio se selecciona un grupo de 200 estudiantes de los cuales todos estudian francés o inglés. De ellos, 70 estudian francés y 150 estudian inglés. ¿Cuántos estudian francés e inglés? 

Respuestas

20

80

70

Retroalimentación

Pregunta

Ejercicio 2.- En otro centro escolar se estudian varios idiomas: francés, inglés, alemán, italiano. Se seleccionan también 200 estudiantes de los cuales, 150 estudian inglés, 70 francés y 40 ambos idiomas. ¿Cuántos estudiantes de ese centro no estudian ni francés ni inglés?

Respuestas

20

40

30

Retroalimentación

Pregunta

Ejercicio 3.- En un instituto de 500 personas se cumple que 300 alumnos juegan al fútbol, 150 juegan al baloncesto, 120 hacen ciclismo, 90 juegan al fútbol y al baloncesto, 20 hacen fútbol y ciclismo, 25 hacen baloncesto y ciclismo, y 3 que por fin practican los tres deportes. 
Si designamos por sus iniciales, los deportes que un alumno practica, C: Ciclismo, F: Fútbol, B: Baloncesto y por $\bar{C},\bar{F},\ \bar{B}$, sus respectivos sucesos complementarios, entonces el siguiente Diagrama de Venn describe la situación del enunciado.

Diagrama de Venn.
Imagen de elaboración propia. Diagrama de Venn. (CC BY-NC-SA)

El suceso $C∩\bar{F}∩\bar{B}$ describiría aquellos alumnos que:

Respuestas

Practican únicamente Ciclismo

Practican Ciclismo y Fútbol

No practica Fútbol y sí Ciclismo

Retroalimentación

Pregunta

Siguiendo en este mismo instituto, ¿cuántos alumnos practican sólo Fútbol y Ciclismo?

Respuestas

20

17

25

Retroalimentación

Pregunta

En este centro se desea saber el numero de practicantes de sólo 2 deportes. Ese número será:

Respuestas

120

135

126

Retroalimentación

Pregunta

En este centro se desea saber también el número de alumnos que no practican ninguno de estos tres deportes. Ese número sería:

Respuestas

60

62

50

Retroalimentación

Pregunta

Ya hemos visto cómo completar el Diagrama de Venn con los cardinales correspondientes a todos los sucesos. Vamos ahora a continuar calculando probabilidades. Para ello, sólo deberás hacer uso de lo aprendido hasta el momento. Imagina que deseamos hallar la probabilidad de que elegido al azar un alumno no haga ningún deporte.
Deberíamos contestar de este modo: $P(\bar{C}∩\bar{F}∩\bar{B})={\Large{\frac{\text{Nº de casos favorables}}{\text{Nº de casos posibles}}}}={\Large{\frac{62}{500}}}=0.124$

Pues bien, siguiendo con este ejemplo, deseamos calcular:
La probabilidad de que elegido al azar un alumno no juegue al baloncesto.

Respuestas

P=0.7

P=0.6

P=0.5

Retroalimentación

Pregunta

Contesta ahora hallando la probabilidad de que elegido al azar un alumno juegue al baloncesto o al fútbol.

Respuestas

P=0.72

P=0.7

P=0.75

Retroalimentación

Pregunta

Por último, calcula la probabilidad de que, elegido al azar un alumno, practique sólo uno de esos deportes.

Respuestas

P=0.25

P=0.35

P=0.618

Retroalimentación

Pregunta

Ejercicio 4.-  De un grupo de 165 diplomáticos, 125 hablan inglés, 80 francés, 50 alemán, 60 hablan ingles y francés, 30 inglés y alemán, 10 francés y alemán y 5 los tres idiomas. Calcular la probabilidad de:

a) Al dirigirte a uno de ellos en francés o alemán te entiendan
b) Que hable inglés y francés pero no alemán
c) Que no hable francés
d) Que hable Francés y no inglés

Respuestas

Hazlo tú ahora, muestra la resolución y compara tus resultados.

Oculta la resolución.

Retroalimentación

Pregunta

Ejercicio 5.- En un grupo de 60 personas, 24 leen la revista A; 22 la B; 20 la C; 6 leen la A y la B; 7 leen la A y la C; 8 leen la B y la C y finalmente 3 leen las tres publicaciones.
Calcular la probabilidad de que elegida una persona al azar:

a) No lea ninguna publicación
b) Lea solo la revista A
c) Lea al menos una de las 3
d) Lean la A o la B

Respuestas

Hazlo tú ahora, muestra la resolución y compara tus resultados.

Oculta la resolución.

Retroalimentación

Opción C: Tablas de contingencia

Resuelve los siguientes ejercicios y expresa los resultados rellenando los huecos con el formato de fracción irreducible p/q. (Fracción simplificada)

Ejercicio 1.-
Se sortea un viaje a Roma entre los 120 mejores clientes de una agencia de automóviles. De ellos, 65 son mujeres, 80 están casados y 45 son mujeres casadas.

Observa cómo podemos usar las tablas de contingencia para registrar y analizar la asociación entre dos o más variables referidas a una misma población.

Sean los sucesos y sus respectivos complementarios de la forma, M=Mujeres, $\bar{M}$ y C=Casadas, $\bar{C}$.

$M$ $\bar{M}$ Total ⇒ $M$ $\bar{M}$ Total
$C$ 45 80 $C$ 45 35 80
$\bar{C}$ $\bar{C}$ 20 20 40
Total 65 120 Total 65 55 120

Una vez completada la tabla, puedes contestar a las siguientes cuestiones.


a) ¿Cuál será la probabilidad de que le toque el viaje a un hombre soltero?
b) Si del afortunado se sabe que es casado, halla la probabilidad de que sea una mujer. 
c) ¿Cuál es la probabilidad de que sea Hombre o Soltero?
d) ¿Cuál es la probabilidad de que sea Mujer?

Se pide que rellenes los huecos con el formato de fracción irreducible p/q.

Ejercicio 2.-
Un taller sabe que por término medio acuden: por la mañana 3 automóviles con problemas eléctricos, 8 con problemas mecánicos y 3 con problemas de chapa, y por la tarde 2 con problemas eléctricos, 3 con problemas mecánicos y 1 con problemas de chapa. Realiza una tabla de contingencia con estos datos y contesta a las siguientes cuestiones:
a) Calcula la probabilidad de acudir al taller por la tarde.
b) Calcula la probabilidad de que se acuda al taller por problemas mecánicos.
c) Se sabe que un automóvil presenta problemas eléctricos, halla la probabilidad de que acuda por la mañana.
d) Calcula la probabilidad de que se tenga un problema mecánico o se acuda por la tarde.

Ejercicio 3.-
Una clase tiene 24 alumnos y todos ellos cursan Inglés y Matemáticas. La mitad aprueban Inglés, 16 aprueban Matemáticas, y 4 suspenden Inglés y Matemáticas. Realiza una tabla de contingencia con los resultados de esta clase. Contesta a las siguientes cuestiones:
a) Calcula la probabilidad de que, al elegir un alumno de esta clase al azar, resulte que aprueba Matemáticas y suspende Inglés.
b) Calcula la probabilidad que haya aprobado sólo una asignatura.
c) Sabiendo que un alumno elegido al azar, haya suspendido sólo una asignatura, sea esta la de Matemáticas.

Habilitar JavaScript

Opción D: Diagramas de árbol

Diagrama de árbol. Permite la representación gráfica de los posibles resultados de un experimento en varios pasos. Nos permite así calcular la probabilidad de que ocurra un evento de una manera muy sencilla. Veamos mejor esto.

Ejemplo. Una fábrica tiene tres cadenas de producción, A, B y C. La cadena A fabrica el 50% del total de los coches producidos; la B, el 30%; y la C, el resto. La probabilidad de que un coche resulte defectuoso en cada una de las cadenas de producción es la siguiente: En la cadena A, 1/2; en la B, 1/4; y en la C, 1/6. Calcula:
a) La probabilidad de que un coche sea defectuoso y haya sido fabricado por la cadena A.
b) La probabilidad de que un coche sea defectuoso.
c) Si un coche no es defectuoso, ¿cuál es la probabilidad de que haya sido producido por la cadena C.

Solución.
Construimos el diagrama de árbol correspondiente. El primer paso que coincide con la primera bifurcación del árbol, corresponderá a la posible elección entre las tres cadenas de producción. Una vez construida esta primera ramificación, continuamos con el siguiente paso para asignar la probabilidad de que sea defectuoso por cada una de las cadenas de producción. Designamos a los sucesos A, B y C como las tres posibles elecciones de producción y al suceso D y su complementario $\bar{D}$ que resulte defectuoso o no defectuoso, respectivamente.
El resultado final será este diagrama: 

Diagrama de árbol: Ejemplo.
Material de elaboración propia. Diagrama de árbol: Ejemplo. (CC BY-NC-SA)

a) La probabilidad de que un coche sea defectuoso y haya sido fabricado por la cadena A.

$P(D∩A)=P(A)·P(D/A)={\Large{\frac{1}{2}}} \cdot {\Large{\frac{1}{2}}}={\Large{\frac{1}{4}}}$

b) La probabilidad de que un coche sea defectuoso.

$P(D)=P(D)·P(D/A)+P(D)·P(D/B)+P(D)·P(D/C)={\Large{\frac{1}{2}}} \cdot {\Large{\frac{1}{2}}} + {\Large{\frac{3}{10}}} \cdot {\Large{\frac{1}{4}}} + {\Large{\frac{1}{5}}} \cdot {\Large{\frac{1}{6}}}={\Large{\frac{43}{120}}} \approx 0.36$


c) Si un coche no es defectuoso, ¿Cuál es la probabilidad de que haya sido producido por la cadena C.

$P(\bar{D})=1-P(D)=1-{\Large{\frac{43}{120}}}={\Large{\frac{77}{120}}}$

Por tanto, $P(C/\bar{D})={\Large{\frac{P(C∩\bar{D})}{P(\bar{D})}}}={\Large{\frac{1/5·5/6}{77/120}}}={\Large{\frac{20}{77}}} \approx 0.26$

Ejercicio.- Pablo planea un viaje para el último fin de semana de junio, eligiendo al azar una de las tres ciudades turísticas que tiene pensado conocer durante el verano. Sin embargo, se pronostica tiempo lluvioso durante esos días. En concreto, las probabilidades de lluvia durante ese fin de semana son de 3/5, 2/7 y 1/4 en las ciudades A, B y C, respectivamente.
a) ¿Cuál es la probabilidad de que no llueva durante su vista?
b) ¿Cuál es la probabilidad de que la ciudad escogida sea B y no llueva durante su visita?
c) Pablo ha sufrido un fin de semana pasado por agua, ¿Cuál es la probabilidad de que haya ido a la ciudad C?

Ver Solución

Solución.-
Designamos por A, B y C a los sucesos que señalan las ciudades turísticas elegidas al azar.
Sean L y $\bar{L}$ respectivamente, los sucesos que pronostican un tiempo de de lluvia o no lluvia, durante ese tiempo de visita turística.

Diagrama de árbol: Solución.
Material de elaboración propia. Diagrama de árbol: Solución.
(CC BY-NC-SA)

a) ¿Cuál es la probabilidad de que no llueva durante su visita?

$P(\bar{L})=P(A)·P(\bar{L}/A)+P(B)·P(\bar{L}/B)+P(C)·P(\bar{L}/C)$

$P(\bar{L})={\Large{\frac{1}{3}}} \cdot {\Large{\frac{2}{5}}} +{\Large{\frac{1}{3}}} \cdot {\Large{\frac{5}{7}}}+{\Large{\frac{1}{3}}} \cdot {\Large{\frac{3}{4}}}={\Large{\frac{87}{140}}} \approx 0.62$ 


b) ¿Cuál es la probabilidad de que la ciudad escogida sea B y no llueva durante su visita?

$P(B∩\bar{L})=P(B)·P(\bar{L}/B)={\Large{\frac{1}{3}}} \cdot {\Large{\frac{5}{7}}}={\Large{\frac{5}{21}}} \approx 0.24$


c) Pablo ha sufrido un fin de semana pasado por agua, ¿cuál es la probabilidad de que haya ido a la ciudad C?

$P(C/L)={\Large{\frac{P(C∩L)}{P(L)}}}={\Large{\frac{P(C∩L)}{1-P(\bar{L})}}}$

$P(C/L)={\Large{\frac{P(C)·P(L/C)}{1-P(\bar{L})}}}={\Large{\frac{1/3·1/4}{1-87/140}}}={\Large{\frac{35}{159}}} \approx 0.22$

Opción E: La probabilidad y su axiomática

Pregunta

1.- Si A y B son dos eventos mutuamente excluyentes, con P(A) = 0.37 y P(B) = 0.44 , se puede afirmar que $P(\bar{A}∩\bar{B})$:

Respuestas

0

0.81

0.19

1

Retroalimentación

Pregunta

2.- Se lanzan un par de dados honestos. La probabilidad de que la suma de los dos números obtenidos sea igual a 10 es equivalente a:

Respuestas

${\Large{\frac{1}{12}}}$

${\Large{\frac{1}{6}}}$

${\Large{\frac{5}{36}}}$

${\Large{\frac{5}{6}}}$

Retroalimentación

Pregunta

3.- Sean A1 , A2 y A3 sucesos de un espacio muestral. El evento “no ocurre ninguno” se expresa como:

Respuestas

$A_1 ∩ A_2 ∩ A_3$

$A_1 ∪ A_2 ∪ A_3$

$\bar{A_1}∩\bar{A_2}∩\bar{A_3}$

Ninguna de las anteriores

Retroalimentación

Pregunta

4.- Se sabe de los eventos A, B y C lo siguiente: $P(A) = P(B) = P(C) = {\Large{\frac{1}{4}}}$ , $P(A ∩ B) = P(C ∩ B) = 0$ y  $P(A ∩ C) ={\Large{\frac{1}{8}}}$.

Halla la probabilidad de que al menos uno de los eventos, A, B o C ocurra.

Respuestas

${\Large{\frac{5}{8}}}$

${\Large{\frac{3}{8}}}$

${\Large{\frac{1}{8}}}$

${\Large{\frac{1}{4}}}$

Retroalimentación

Pregunta

5.- Sean A, B y C tres eventos tales que $P(A) = 0.4$,  $P(B)= 0.3$,  $P(A∩B)= 0.1$,  $P(A∩C)= 0.1$,  $P(B∩C)= 0$, y  $P(A∪C)= 0.7$. 

Determina la probabilidad de que ocurra exactamente solo uno de dichos eventos.

Respuestas

0.5

0.3

0.2

0.7

Retroalimentación

Pregunta

6.- Sean A y B eventos independientes, tales que con probabilidad ${\Large{\frac{1}{6}}}$ ocurren simultáneamente, y con probabilidad ${\Large{\frac{1}{3}}}$ ninguno de ellos ocurre.

Halla P(A) y P(B).

Respuestas

${\Large{\frac{1}{3}}}$ y ${\Large{\frac{1}{2}}}$

${\Large{\frac{1}{4}}}$ y ${\Large{\frac{1}{2}}}$

${\Large{\frac{1}{3}}}$ y ${\Large{\frac{1}{4}}}$

Ninguna de las anteriores

Retroalimentación

Pregunta

7.- Sea $E=\{a, b, c, d, e \}$, con $P(a) ={\Large{\frac{1}{8}}}$, $P(b)={\Large{\frac{1}{16}}}$, $P(c) ={\Large{\frac{3}{16}}}$, $P(d) ={\Large{\frac{5}{16}}}$, y $P(e) ={\Large{\frac{5}{16}}}$.

Sean los eventos  $A = \{a, d, e\}$ y $B = \{c, d, e\}$.

Calcula $P \left( B/\bar{A} \right)$:

Respuestas

${\Large{\frac{1}{4}}}$

${\Large{\frac{1}{8}}}$

${\Large{\frac{3}{4}}}$

Ninguna de las anteriores

Retroalimentación

Pregunta

8.- Sean A y B eventos independientes tales que $P(A) ={\Large{\frac{1}{3}}}$ y $P(A∪B) ={\Large{\frac{2}{3}}}$. Calcula $P(B)$

Respuestas

${\Large{\frac{1}{2}}}$

${\Large{\frac{1}{3}}}$

${\Large{\frac{3}{4}}}$

${\Large{\frac{1}{4}}}$

Retroalimentación

Página 3 de 12

Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0

Creado con eXeLearning (Ventana nueva)