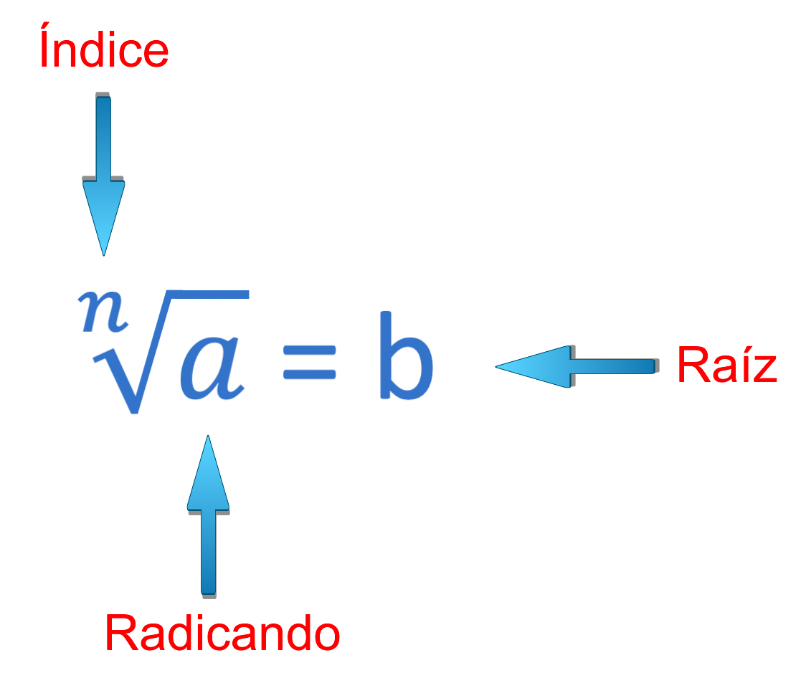
1. Radicación
En ocasiones es posible operar con valores exactos de números reales. Esto se consigue utilizando la representación simbólica de estos números. Es el caso de los radicales, que los puedes manipular fácilmente mediante sus propiedades, lo que permite simplificar expresiones de forma sencilla.
Podemos entender la radicación como la operación inversa a la potenciación. Para reforzar esta idea vas a ver un ejemplo. Supón que deseas hallar el volumen de un cubo de lado 2 m. Sabes que el volumen viene dado por la expresión V = l3 donde l representa la longitud del lado. Por consiguiente, tienes que V = 23 = 8 m3 .
Pero imagina que te interesa calcular la longitud del lado del cubo para que el volumen sea 8. En este caso te encuentras con esta expresión: V = l3 , 8 = l3 . Es decir, tienes que calcular un número l que al elevarlo al cubo obtengas 8. Este número es, por definición, la raíz cúbica de 3.
Volviendo al primer ejemplo, 2 (longitud del lado del cubo) es por definición la raíz cúbica de 8, ya que 23 = 8.
En general, si cualquier número a es elevado a 3 y al resultados le hallamos la raíz cúbica obtendremos el número de partida a.