1. Los números en la vida cotidiana
En la vida cotidiana es habitual utilizar valores aproximados en lugar de exactos. Esto queda justificado porque las herramientas y dispositivos que utilizas para medir tienen un límite de precisión o sensibilidad, pero, también, porque sería poco útil por irrelevante.
Por ejemplo, si te preguntan por el precio del coche que has comprado y por el que has pagado 14.290€, normalmente dices que te ha costado 14.000€. La diferencia de 290 € parece poco importante respecto al precio real.
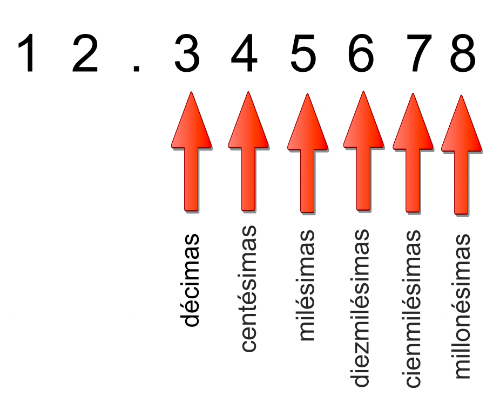
Vas a recordar cómo se leen los números decimales.