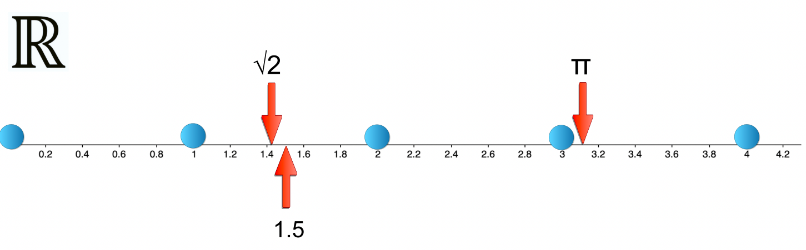
1. Recta real
Si te dan dos números distintos cualesquiera, ya sean racionales o irracionales, siempre hay uno que es menor que el otro. Por otro lado, entre dos números reales diferentes existen una cantidad infinita de números reales. Esta propiedad te permite ordenarlos y representarlos sobre una recta que se llamará recta real.
Además, esta recta está llena de números, no contiene huecos, de tal manera que a cada número real le corresponde un punto de la recta y viceversa, a cada punto de la recta le corresponde un número real.