4.3 Magnitudes de interés
Cuando analizamos el lanzamiento oblicuo, es interesante conocer el tiempo de vuelo, tv, la altura máxima que alcanza, ym, y la distancia horizontal recorrida o alcance horizontal, xm.
 Captura de pantalla de animación de Jesús Peñas en Educaplus
Captura de pantalla de animación de Jesús Peñas en Educaplus
Tiempo de vuelo
Si eliges el origen del sistema de referencia tal que xo = 0 e yo = 0, puedes calcular el tiempo que el proyectil permanece en el aire hasta llegar al suelo, que se suele llamar tiempo de vuelo, tv.
|
|
| Imagen de elaboración propia |
Como la trayectoria es simétrica puedes calcular el tiempo necesario para llegar al punto más alto y multiplicarlo por dos.
En este punto la componente vertical de la velocidad se anula, vy = 0, y nos queda:
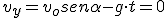
y despejando, el tiempo de vuelo será:
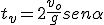
Altura máxima
La altura máxima se alcanza cuando la componente vertical vy de la velocidad se hace cero.
Como has calculado en el párrafo anterior, el tiempo necesario para que el proyectil llegue al punto más alto es 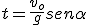 y el valor de la altura máxima será:
y el valor de la altura máxima será:
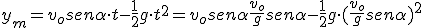
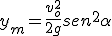
Alcance máximo
Como el tiempo de vuelo es el necesario para llegar al suelo, si sustituyes ese tiempo en
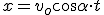
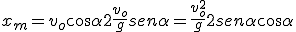
Si recuerdas la identidad trigonométrica: 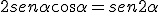 el alcance máximo es:
el alcance máximo es:
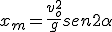
El valor máximo de alcance se da cuando  , igualdad que se cumple para un ángulo
, igualdad que se cumple para un ángulo 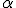 =45º.
=45º.
No hay que memorizar estas fórmulas anteriores, ya que si en una situación dada hay que determinar cualquiera de ellas, se calculan sustituyendo en las ecuaciones generales del movimiento de que se trate.
Importante
El ángulo de lanzamiento para que el alcance sea máximo es de 45º.
Caso práctico
Un saltador de longitud alcanza la velocidad de 10 m/s después de su carrera, cuando inicia su salto con un ángulo de 30º con respecto a la horizontal. Determina:
a) el tiempo total que permanece en el aire.
b) la altura máxima alcanzada en su salto.
c) la marca que consigue el saltador (longitud del salto).
