4.2 Lanzamiento horizontal
Es un caso particular del lanzamiento de proyectiles que tiene lugar cuando un objeto (sometido a la acción de la gravedad) es lanzado con determinada velocidad inicial v0 en dirección paralela al suelo, es decir que la velocidad inicial solo tiene componente X .
Si suponemos que no hay resistencia del aire, el movimiento es el resultante de la composición de dos movimientos:
- Uno uniforme según el eje X.
- Otro uniformemente acelerado según el eje Y.
Las ecuaciones del movimiento son:
| En el eje X | En el eje Y |
| ax = 0 | ay = -g |
| vx = v0 = constante | vy = -g·t |
| x = x0 + v0·t | y = y0 - 1/2·g·t2 |
También podemos expresar las ecuaciones del movimiento en forma vectorial.
Para la velocidad en cualquier instante tenemos:
Y la ecuación de la posición en cualquier instante es:
Podremos encontrar la ecuación de la trayectoria eliminando el tiempo entre las ecuaciones (componentes del vector r):
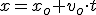
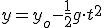
y, considerando xo = 0, nos queda:
que es una ecuación de segundo grado que representa la ecuación de una parábola.
Caso práctico
Un jugador de tenis situado a 12 m de la red, pretende hacer un tanto de saque (ace), para lo cual la bola tiene que botar a 6,4 m de la red, en campo contrario. Golpea la pelota a 2,30 m de altura, en dirección horizontal, con una velocidad de 108 km/h. Si la red se levanta hasta 90 cm de altura, ¿conseguirá su propósito el jugador?
En la siguiente simulación se lanza un objeto horizontalmente desde una altura de 12 m con una velocidad inicial de 20 m/s.
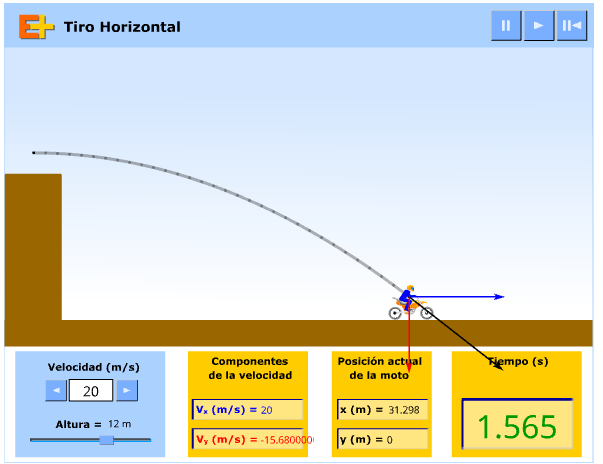Captura de pantalla de animación de Jesús Peñas en Educaplus
Utilizando las ecuaciones comprueba que los datos proporcionados por el simulador son correctos.