3. Progresiones geométricas
 |
| Imagen en Flickr de jefedo61 bajo CC |
Existe una leyenda sobre el supuesto inventor del juego del ajedrez, Sissa Ben Dahir. Cierto rey hindú se encontraba muy triste debido a la muerte de su hijo. Para aliviar su pena, Sissa le enseñó a jugar al ajedrez.
Quedó tan contento el monarca que le ofreció el regalo que él quisiera. Sissa tan sólo le pidió que le diera un grano de trigo por la primera casilla del tablero de ajedrez, el doble por la segunda, el doble por la tercera y así sucesivamente hasta completar las 64 casillas.
El rey accedió entre satisfecho y sorprendido a la extraña petición, pero al realizar los cálculos se dio cuenta de que le sería imposible cumplirla.
El número de granos de arroz que corresponde a cada una de las casillas es una sucesión numérica:
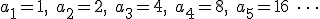
El primer término es 1, los términos posteriores se obtienen multiplicando por 2 el término anterior, es decir:
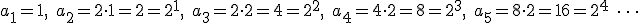
Podríamos escribir lo anterior de la siguiente forma: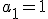 
y 
.
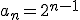Esto nos permite saber cómodamente el número de granos de la última casilla, la 64:
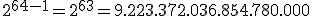granos de trigo.
Es decir, 
granos. Y aún tendríamos que sumar todos los granos de las 64 casillas.
¿Entiendes ahora cómo se quedó el rey cuando se dio cuenta del regalo que le debía a Sissa?
A este tipo de sucesiones se les denomina progresiones geométricas.
Importante
Se llama progresión geométrica a toda sucesión en la que cada término, exceptuando el primero, es el producto del anterior por una cantidad fija llamada razón.
Es decir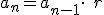 
, donde 
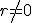es la razón, y 
.
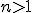En la progresión geométrica de los granos de trigo la razón es 2, un número mayor que 1 en valor absoluto. Esto implica que los términos de la progresión se vayan haciendo muy grande en valor absoluto, como hemos podido comprobar con los granos que habría que poner en la casilla 64.
Pero también podemos considerar progresiones geométricas en que la razón es número menor que 1 en valor absoluto. Observa con detenimiento la siguiente presentación.
La progresión geométrica anterior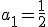 
, la razón 
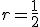, y el término general 
.
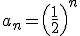Ya veremos cómo podemos calcular las sumas de las dos progresiones geométricas anteriores.
Al igual que ocurre con las progresiones aritméticas, existe una ley de formación para las geométricas.
Importante
Una progresión geométrica cuyo primer término es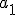 
y de razón 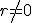, tiene como término general:
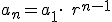
Caso de estudio
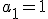y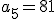 
.
Actividad de rellenar huecos
|
| Imagen en Flickr de sergis blog bajo CC |
Interpola tres medios geométricos entre 3 y 48.
Interpolar tres medios geométricos entre dos números a y b quiere decir intercalar tres números c, d y e entre a y b, de tal forma que los cinco números a, c, d, e y b formen una progresión geométrica.
Este problema se puede extender a cualquier cantidad de números entre dos números conocidos. Por ejemplo, interpolar seis medios geométricos entre a y b quiere decir intercalar seis números entre ellos, de tal forma que los ocho números, ordenados de menor a mayor, formen una progresión geométrica.
Para saber más sobre interpolación geométrica puedes ir a este enlace.
Del mismo modo que ocurría con una progresión aritmética, también nos puede interesar en algunas ocasiones saber cuánto vale la suma de los términos de una progresión geométrica. Por ejemplo para saber cuántos granos de trigo debería entregar el rey a Sissa o demostrar que la suma de las potencias de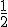 
vale 1.
Veamos cuáles son las fórmulas que nos permiten sumar algunos o muchos términos de una progresión geométrica.
Actividad
-
La suma de los
primeros términos de una progresión geométrica de razón 
es igual a: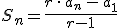 
-
Si la razón es, en valor absoluto, menor que 1,
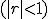la suma de los infinitos términos de la progresión geométrica toma un valor finito y se calcula utilizando la fórmula: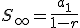 
Caso de estudio
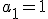y 
.
Caso de estudio
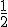es 1.
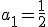y 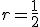, por tanto .
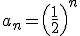Caso práctico
 |
Curso 2013/2014
El término a10 de una progresión geométrica de razón 2 es 2560. Halle el término a14¿Cuánto vale la suma de los 14 primeros términos?