1.1. Conceptos básicos

¿Te gustan los pasatiempos? En general son pequeños divertimentos lógicos que nos hacen pensar y nos evaden durante cierto tiempo de la realidad.

¿A ver si eres capaz de adivinar este que te proponemos?

Los números de la siguiente secuencia tienen relación con las figuras que lo rodean, sabrías decir cuál falta.

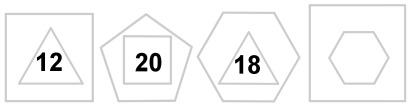Imagen de elaboración propia

La anterior es una secuencia numérica que a pesar de poseer una regla para conocer cada valor individualmente, no tiene una regla de formación general. Para nosotros esas serán las secuencias que nos interesan, las que cumplen una norma para su construcción.

Esto ocurre con los denominados números poligonales. El ejemplo más sencillo de ellos son los números triangulares. En la siguiente imagen puedes ver cómo se van construyendo.

Imagen de elaboración propia

¿Sabrías decir cómo continúa la secuencia, cuáles son el quinto y sexto número triangular? ¿Y el décimo? ¿Serías capaz de dar una regla general para construirlos todos?

De todo esto trata el estudio de las sucesiones numéricas, y a dar respuestas a este tipo de preguntas está dedicado el tema.

Caso de estudio

En este enlace puedes acceder a una recopilación de pasatiempos numéricos. La mayoría de ellos son secuencias numéricas. Todos son entretenidos, pero nos conformamos con que resuelvas el 1a, el 3 completo y el 6.

Te recomendamos que escribas en un papel las diferentes sucesiones numéricas, y analices con detenimiento qué relación existe entre cada término y el anterior.

Retroalimentación

1a) La secuencia es 0, 3, 8, 15, 24... Estudiemos las diferencias entre cada término y el anterior. Estas vuelven a ser otra secuencia: 3, 5, 7 y 9. La siguiente diferencia será 11, por tanto, el siguiente término será 35.

3a) La secuencia es 60, 63, 57, 66, 54, 69, 51, 72... Si nos fijamos, los términos impares se incrementan en 3 unidades, en tanto que los pares disminuyen en 3. El término que nos piden es el que ocupa el lugar octavo, par, por tanto será 72, que se obtiene de sumar 3 a 69.

3b) 1, 5, 14, 30, 55, 91, 140... Las diferencias entre dos números consecutivos generan la siguiente secuencia: 4, 9, 16, 25, 36, 49. Esta corresponde al cuadrado de los primeros números naturales. La siguiente sería el cuadrado de 8, es decir, 64. Lo sumamos a 140 y obtenemos 204, que será el término que nos piden.

6) 2, 6, 30, 210, 2310... En este caso, cada término se obtiene del anterior multiplicado por un número, la secuencia de dichos números es 3, 5, 7... Y aquí creo que hay un fallo, porque el siguiente es 9, por tanto el término quinto sería 210·9 = 1890. Pero aparece 2310 que es igual a 210·11, de ahí lo del fallo.

Importante

Una sucesión numérica es todo conjunto ordenado de números reales.

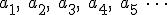
Cada uno de los elementos de la sucesión se llama término. Como puedes ver, se utilizan los subíndices para conocer el lugar que ocupa cada término en la sucesión.

Se llama término general al que ocupa el lugar indeterminado . Dicho término se expresa como .

En muchas ocasiones, los términos de las sucesiones se pueden determinar a partir de cierto criterio, este criterio se denomina regla de formación.

En el caso de números triangulares, tendríamos que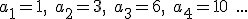

Más adelante veremos por qué, pero puedes comprobar que el término general de la sucesión formada por los números triangulares es .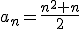

Veamos que es cierto para el término que ocupa el segundo lugar: .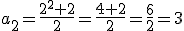

Esa expresión es la regla de formación de los números triangulares que nos permite saber el valor de cualquier término, ocupe el lugar que ocupe. Por ejemplo, el término que ocupa el lugar 100: .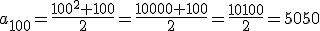

No siempre es posible escribir el término general de una sucesión con una expresión algebraica, aunque conozcamos la regla que sirve para hallar sus términos. Es el caso de las sucesiones recurrentes, en las que cada término queda determinado a partir de los anteriores. La ya mencionada sucesión de Fibonacci es de este tipo. Recuerda, 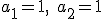, y a partir del tercer término se cumple que 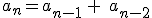, es decir cada término es la suma de los dos anteriores.

Aplicando la regla de recurrencia anterior tenemos que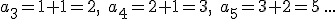

Si haces clic en el siguiente enlace, puedes acceder a los contenidos del Proyecto EDAD en los que se desarrollan los conceptos anteriores, acompañados de algunos ejemplos y ejercicios.

Recurso de Miguel Ángel Cabezón Ochoa en Red Educativa Digital DESCARTES. Licencia CC

Actividad de rellenar huecos

Recuerdas las tres primeras sucesiones que vimos al principio del tema:

Los números naturales: 1, 2, 3, 4, 5...

La tabla de multiplicar del 7: 7, 14, 21, 28, 35...

Los cuadrados de los números naturales: 1, 4, 9, 16, 25...

Completa las siguientes frases.