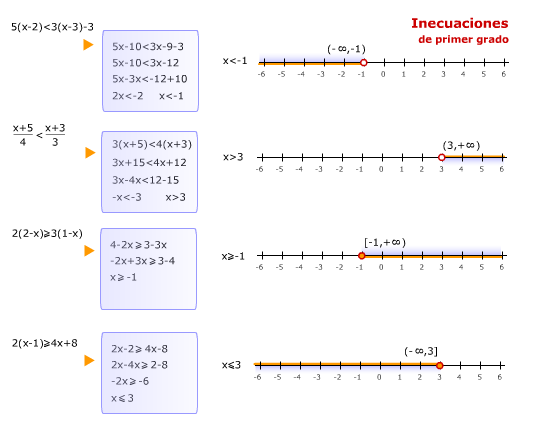
1.1. Veamos cómo podemos representar la solución

Fotografía en Flickr de Gonzopowers bajo licencia Creative Commons

Seguramente, estarás acostumbrado o acostumbrada a utilizar las Matemáticas en un montón de situaciones que se presentan en el día a día, aunque no seas consciente de ello, y en muchos casos estarás resolviendo ecuaciones.

Te cuento lo que le pasó a Pedro, ¿te acuerdas?, el Director de Personal de TRANS VELOX.

Los fines de semana, coge su moto, que por cierto, ¡vaya moto!, y se para a echarle gasolina. El sábado pasado se miró el bolsillo y sólo tenía 10 € y el litro valía 1,25 €, ¿cuántos litros pudo echarle?

Después, le entró hambre y fue a comprar a una tienda 1/4 de mortadela; en el mostrador ponía que el Kg valía 5,70 €, y le quedaba sólo 1 €, ¿cuántos gramos pudo pedir?

En definitiva, muchas veces tienes que resolver ecuaciones de primer grado en las que obtienes una única solución.

Además, recuerda que para representar esta solución, en Matemáticas, tienes que dibujar un punto sobre la recta numérica.

Como te habrás dado cuenta, no siempre tenemos que resolver ecuaciones, es decir, expresiones donde aparezcan igualdades, sino que la mayoría de las veces, lo que aparecen son desigualdades, y entonces tenemos que hablar de inecuaciones.

Si con la moto queremos gastar como mucho 10 €, estamos diciendo que queremos saber cuántos litros podemos echar como mucho, es decir:

Si x es el número de litros máximo que podemos echar, tendríamos que 1,25·x≤10, y despejando x, tenemos que x≤8, es decir, tenemos que echar 8 litros o menos de 8.

Como en este caso, x no puede ser negativo, la solución la escribiríamos utilizando el siguiente intervalo [0,8], es decir, x está en ese intervalo.

Recuerda: Un intervalo es un subconjunto conexo de la recta real definido por sus extremos a y b. Según éstos pertenezcan o no al intervalo hablaremos respectivamente de intervalo cerrado [a,b], intervalo abierto (a,b), e intervalo semiabierto [a,b) ó (a,b].