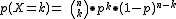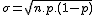Resumen
Importante
Una variable aleatoria es una función que asocia a cada elemento del espacio muestral un número real. Por lo tanto, toma valores numéricos reales que vienen dados por el resultado de un experimento aleatorio.
Por ejemplo, el número de pacientes que atiende un médico en la consulta durante una semana, el tiempo que esperamos para pagar en la caja de un supermercado, el número de llamadas al 112 en el transcurso de una hora, ...
Las variables aleatorias se simbolizan con letras mayúsculas (X, Y, Z).
Las variables aleatorias, dependiendo de los valores que toman, pueden clasificarse en:
Variables discretas: Son aquellas que, aunque también puedan tomar valores infinitos, entre un valor y el siguiente no es necesario pasar por los puntos intermedios. Suelen estar asociadas a experimentos aleatorios en que se cuenta algo.
Ejemplo: El número de monedas en una mano de los chinos puede ser 2 y en otra 3, sin embargo, nunca tomará ningún valor entre 2 y 3.
Variables continuas: Pueden tomar todos los valores de un intervalo. Son aquellas en las que necesariamente, para pasar de un valor a otro, deben tomar los infinitos valores intermedios entre ellos. Suelen estar asociadas a experimentos aleatorios en que se mide algo.
Ejemplo: Si dos personas pesan exactamente 55 y 60 kg, entre ellas pueden haber personas que pesen 55,2 kg, otra que pese 57,4 kg, otra con 58 kg, ...
Importante
Suponemos que tenemos una variable aleatoria discreta X con valores x1, x2, …., xk, y
conocemos las siguientes probabilidades p(X= x1) = p1, p(X= x2) = p2, ….., p(X= xk) = pk.
Se define su función de probabilidad como la ley o aplicación que asocia a cada valor xi su probabilidad p(X=xi)=pi,
verificando:
1) Son siempre positivas: pi > o
2) La suma de todas, es igual a uno: p1+ p2+ p3+ ……..+ pK = 1
Dada una variable aleatoria discreta (X) se define su función de distribución como:
F(x) = p( X ≤ x), que asocia a cada número (x) la probabilidad acumulada hasta él.
Importante
Dada una variable aleatoria discreta, X, que toma los valores: x1, x2, x3, ... , xk y dada su función de probabilidad asociada:
p(X=xi) = pi, podemos calcularle los siguientes parámetros, cuyas fórmulas se detallan:
Media o esperanza matemática: 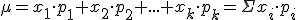 (También se representa como E(x))
(También se representa como E(x))
Puede interpretarse como el valor esperado o medio que toma la variable o, tambien, como el valor central de la distribución.
Varianza: 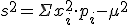 (También se representa con Var(X) o V(x))
(También se representa con Var(X) o V(x))
Desviación típica: 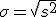 (También se representa por DT(x))
(También se representa por DT(x))
Importante
Una variable aleatoria discreta sigue una binomial si:
1º) Hay un experimento aleatorio que se repite n veces con independencia (Tener n=6 hijos, el sexo de cada uno es independiente del anterior, contestar un test de n=30 preguntas el acierto o no, no depende de la cuestión anterior).
2º) En cada prueba solo puede darse dos situaciones: éxito o fracaso (ser varón o no, acertar o no). Las probabilidades de ambos suman uno pero no tienen que ser la misma.
p= probabilidad de obtener éxito
1-p= probabilidad de no obtener éxito (fracaso).
3º) La variable se define como el número de éxitos conseguidos: X = número de éxitos conseguidos en los n experimentos.
Para simplificar, en adelante designamos por B(n,p) a la distribución binomial de parámetro n (veces que se repite el experimento) y p (probabilidad de éxito)

Importante
El número combinatorio:
Es el número de combinaciones distintas de k elementos que se pueden formar con n elementos.
Propiedades:
1) 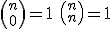
2) 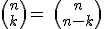
Importante