3.2. Parámetros de la distribución binomial

En el apartado 2.3, ya se ha comentado que cada variable aleatoria se caracteriza por sus parámetros. La B(n, p) no va ha ser distinta a las demás.

¿Recuerdas la tabla de la variable aleatoria que designaba el número de vehículos destinados a taxis?

X	0	1	2	3
p_i	0,729	0,243	0,027	0,001

Recordando las fórmulas de la esperanza, varianza y la desviación típica, tendremos:

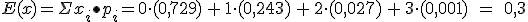
Observa que E(x)= 3·(0,1) = n·p

De la misma forma para la varianza:

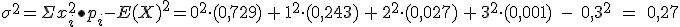
También, la varianza depende de n y p, es decir , n·p·(1-p)=3·(0,1)·(0,9) = 0,27.

El resultado de estas conclusiones lo vamos a ver en el siguiente cuadro resumen de la Binomial. ( Recuerda q=1-p)

Media o esperanza matemática	μ=n·p
Varianza	σ²=n·p·q
Desviación típica	σ=√σ²

Importante

Resumen de una Binomial

Si una variable aleatoria X sigue una binomial de parámetros n y p; B(n, p) podemos decir:

1) n es el número de pruebas independientes.

2) p es la probabilidad de obtener un éxito y por tanto 1-p la probabilidad de fracaso.

3) X = número de éxitos obtenidos en las n pruebas.

4) La función de probabilidad es

5) La media E(X)=n·p

6) La varianza

7) La desviación típica

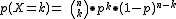
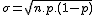
Ejemplos:

A continuación te ofrecemos un vídeo. En él encontrarás problemas sobre la binomial:

Vídeo de lasmatematicas.es alojado en Youtube

Caso práctico

Imagen avión

Imagen de OpenClipart-Vectors en Pixabay. Pixabay License

La probabilidad de que un avión llegue con retraso a un determinado aeropuerto es de 0,012. En una hora llegan al aeropuerto 8 aviones. ¿Cuál es la probabilidad que ninguno llegue con retraso? ¿Cuál es la probabilidad de que alguno llegue con retraso? ¿y cuál es la probabilidad de que lleguen dos o menos con retraso?

Si en un día se esperan la llegada de 120 aviones ¿qué media de aviones llegarán con retraso? ¿Cuál sería en este caso la desviación típica?