3.1. Números combinatorios
Factorial de un número natural
Se define factorial de n y lo denotamos por n! al producto de todos los números naturales positivos menores o iguales que n.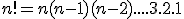 
En el dibujo observarás tres ejemplos: 3!=3.2.1=6; 4!=4.3.2.1=24 y 8!=8.7.6.5.4.3.2.1=40.320Prueba en tu calculadora (tecla !) y verás como caso curioso que 0!=1.
Número combinatorio Se define número combinatorio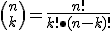 
y representa, como bien sabes por el apartado anterior, el número de casos distintos de k éxitos en n experimentos.
En el ejercicio del apartado anterior, "Taxis de la marca TOMOYA", el número de casos que la variable toma el valor 2 es de tres. Calculándolo con el número combinatorio sería: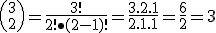
Importante
El número combinatorio:
Es el número de combinaciones distintas de k elementos que se pueden formar con n elementos.
Propiedades:
1) 
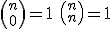
2) 
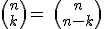
Reflexiona
¿Cuántas combinaciones posibles tiene la primitiva? (Te recuerdo que hay en el bombo 49 bolas y que cada combinación consta de 6 bolas.)
Curiosidad
Triángulo de Tartaglia
Hoy en día, con la utilización de la calculadora, es fácil calcular cualquier número combinatorio, sin embargo, resulta bastante interesante el cálculo de números combinatorios con el siguiente triángulo, conocido entre otros nombres como Triángulo de Tartaglia, en la que cada número combinatorio se obtiene sumando los dos que tiene encima. En la siguiente imagen aparecen las siete primeras filas.
Por ejemplo, para calcular el número combinatorio 
, sumamos el valor de los números combinatorios que están sobre él, esto es, 
.