2.3. Parámetros
En la Unidad en la que se desarrolla el estudio de las variables estadísticas, se explica cómo calcular las medidas asociadas a una de estas variables: media, mediana, varianza o desviación típica. A las variables aleatorias (que estamos estudiando en esta unidad) también le calcularemos medidas. Incluso, coincidirán con los nombres de las medidas de las variables estadísticas. Es por ello que, para evitar confusiones, en vez de medidas, utilizaremos el nombre de parámetros.
Imagen de kreatikar en Pixabay. Dominio Público
¿Cuántas veces oímos en los medios de comunicación la esperanza de vida de los españoles es de...?
¿Qué son los parámetros de una variable aleatoria? ¿Para qué nos sirven?
Los parámetros en las variables aleatorias son como para las personas el DNI, nombre y apellidos. Sus parámetros las identifican, para bien o para mal, de las demás.
Importante
Dada una variable aleatoria discreta, X, que toma los valores: x1, x2, x3, ... , xk y dada su función de probabilidad asociada:
p(X=xi) = pi, podemos calcularle los siguientes parámetros, cuyas fórmulas se detallan:
Media o esperanza matemática: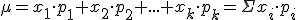 
(También se representa como E(x))
Puede interpretarse como el valor esperado o medio que toma la variable o, tambien, como el valor central de la distribución.
Varianza: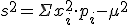 
(También se representa con Var(X) o V(x))
Desviación típica: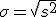 
(También se representa por DT(x))
Caso práctico
Usando los datos del juego de los Chinos:
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | Sumas |
| pi | 1/16 | 2/16 | 3/16 | 4/16 | 3/16 | 2/16 | 1/16 |  |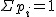
| x.pi | 0 | 2/16 | 6/16 | 12/16 | 12/16 | 10/16 | 6/16 |  |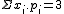
| x2.pi | 0 | 2/16 | 24/16 | 36/16 | 48/16 | 50/16 | 3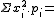6/16 |  196/16 |
Vamos a calcular la esperanza, varianza y desviación típica del juego de los chinos.
Observa que se ha completado la tabla con dos filas y hemos calculado las sumas de las filas.
Aplicando las fórmulas para cada uno de los parámetros tendríamos:
Esperanza:
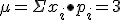
Varianza:
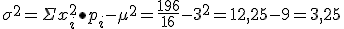
Desviación típica:
