2.2. Función de probabilidad
Si recuerdas, en la unidad anterior, cuando teníamos una variable estadística, también disponíamos de su distribución de frecuencias que presentamos en una tabla. Del mismo modo, para una variable aleatoria, tendremos su distribución de probabilidad. En este caso, en vez de con frecuencias trabajaremos con probabilidades.
Importante
Suponemos que tenemos una variable aleatoria discreta X con valores x1, x2, …., xk, y
conocemos las siguientes probabilidades p(X= x1) = p1, p(X= x2) = p2, ….., p(X= xk) = pk.
Se define su función de probabilidad como la ley o aplicación que asocia a cada valor xi su probabilidad p(X=xi)=pi,
verificando:
1) Son siempre positivas: pi > o
2) La suma de todas, es igual a uno: p1+ p2+ p3+ ……..+ pK = 1
Ejemplo:
Veamos cómo se concreta en el juego de los chinos las definiciones del "Importante" anterior.
La siguiente tabla recoge la distribución de frecuencias y la probabilidad que tiene cada uno de los números que resulta de sumar la monedas. A saber:
- xi representa cada uno de los posibles valores que puede tomar la variable X: "n.º de monedas totales"
- p(xi) es la probabilidad (frecuencia relativa) de que la variable X tome el valor xi
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| frecuencia absoluta | 1 | 2 | 3 | 4 | 3 | 2 | 1 |
| p(xi) | 1/16 | 2/16 | 3/16 | 4/16 | 3/16 | 2/16 | 1/16 |
Caso práctico

Consideremos la variable aleatoria X="número de caras obtenidas al lanzar tres veces una moneda"
(a) Indica los posibles valores X=xi que puede tomar la variable X.
(b) Determina el espacio muestral, E.
(c) Calcula la función de probabilidad, p(X=xi), de la variable X.
Importante
Dada una variable aleatoria discreta (X) se define su función de distribución como:
F(x) = p( X ≤ x), que asocia a cada número (x) la probabilidad acumulada hasta él.
Comprueba lo aprendido
Seguimos trabajando con la función de distribución de la variable X="número de caras obtenidas al lanzar tres veces una moneda".
Basándote en su función de probabilidad, p(X=xi), obtenida en el apartado (c) del ejercicio anterior, marca Verdadero o Falso en cada caso.
p(X=x1)=p(X=0)=1/8=0,125
p(X=x2)=p(X=1)=3/8=0,375
p(X=x3)=p(X=2)=3/8=0,375
p(X=x4)=p(X=3)=1/8=0,125
Retroalimentación
Falso
p(X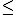 2) = p(X=0) + p(X=1) + p(X=2) = 0,125 + 0,375 + 0,375 = 0,875
2) = p(X=0) + p(X=1) + p(X=2) = 0,125 + 0,375 + 0,375 = 0,875
Retroalimentación
Verdadero
p(X<2) = p(X=0) + p(X=1) = 0,125 + 0,375 = 0,5