1. Conceptos básicos
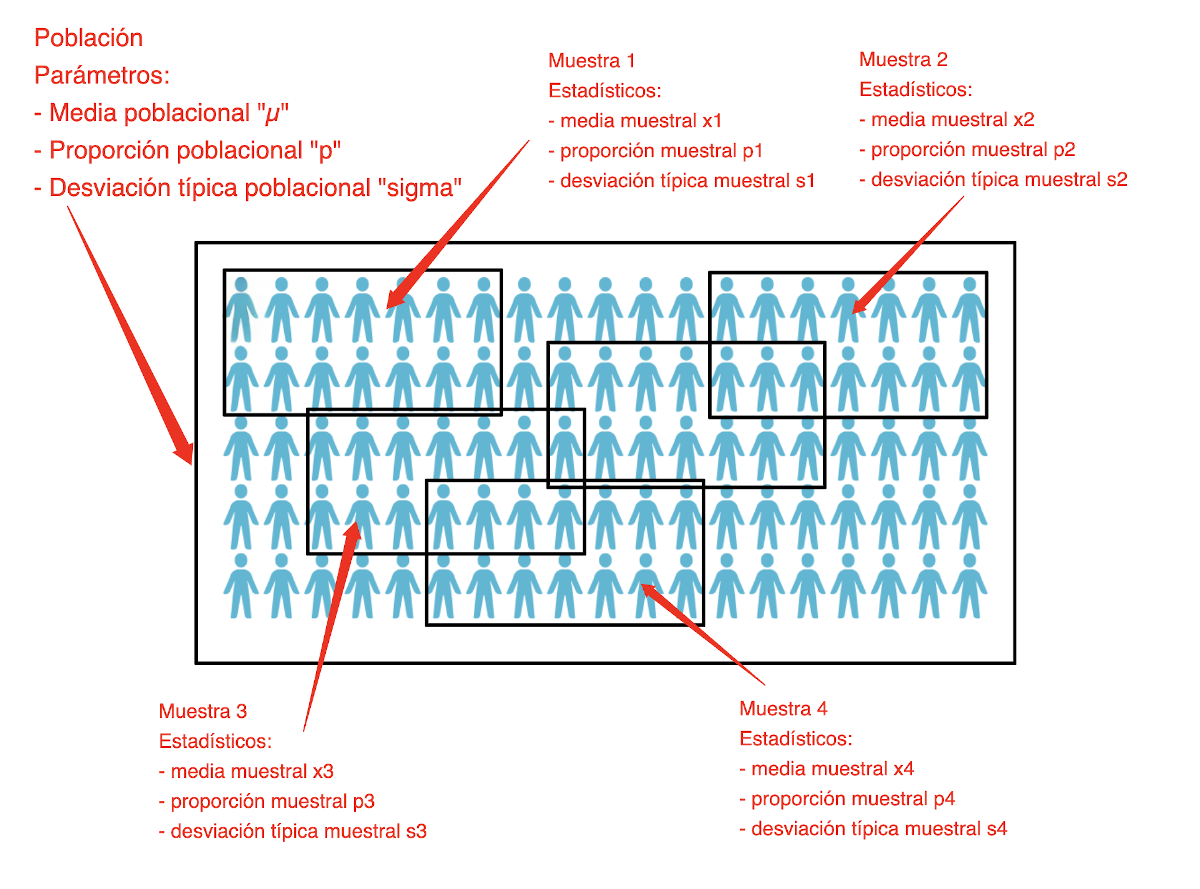
1. Población y Muestra
Población: La población se define como el conjunto total de elementos o individuos que comparten características específicas objeto de estudio. Por ejemplo, si nuestro interés radica en analizar los hábitos alimenticios de los estudiantes universitarios, la población correspondería a todos los estudiantes de dicha institución. Esta población representa el grupo completo del que se desea obtener información o sobre el cual se pretenden realizar generalizaciones.
Muestra: La muestra es un subconjunto de la población. Este subconjunto se selecciona para realizar el estudio porque trabajar con toda la población es generalmente impracticable. Es esencial que la muestra sea representativa de la población para que las conclusiones del estudio sean válidas.
2. Parámetro y Estadístico
Parámetro: Un parámetro es una medida descriptiva que resume alguna característica de la población completa. Ejemplos de parámetros incluyen la media poblacional (\(\mu\)), la varianza poblacional (\(\sigma^2\)), y la proporción poblacional (p). Los parámetros son generalmente desconocidos porque es difícil o imposible medir a toda la población.
Estadístico: Un estadístico es una medida descriptiva calculada a partir de una muestra. Ejemplos de estadísticos incluyen la media muestral (\(\bar{x}\)), la varianza muestral $(s^2)$, y la proporción muestral (\(\hat{p}\)). Los estadísticos se utilizan como estimaciones de los parámetros de la población.
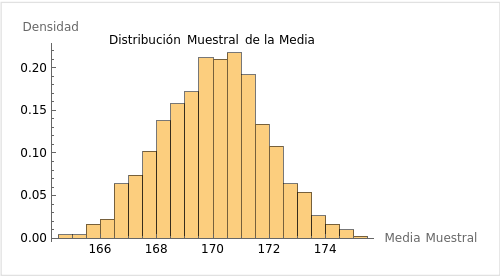
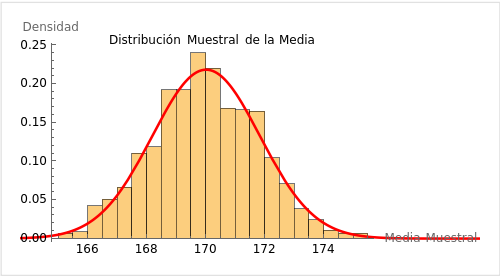
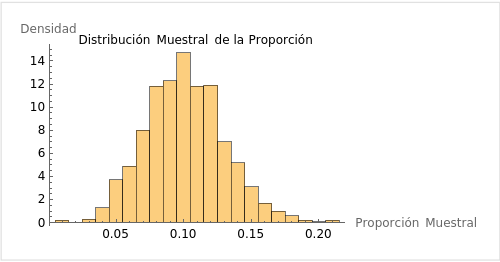
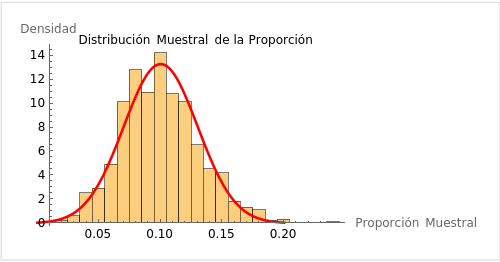
3. Distribución Muestral
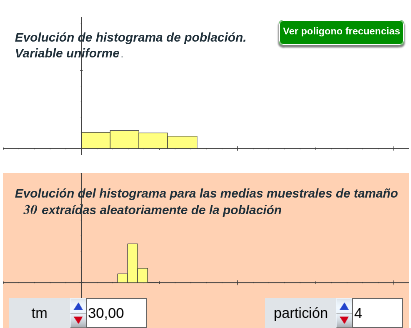
Una distribución muestral es la distribución de un estadístico (como la media, la proporción o la varianza) calculado a partir de muchas muestras diferentes de una población. Por ejemplo, si tomamos múltiples muestras de estudiantes y calculamos la media de cada muestra, la distribución de estas medias muestrales es una distribución muestral.
Esta distribución nos ayuda a entender la variabilidad de los estadísticos muestrales y nos proporciona una base para hacer inferencias sobre la población.