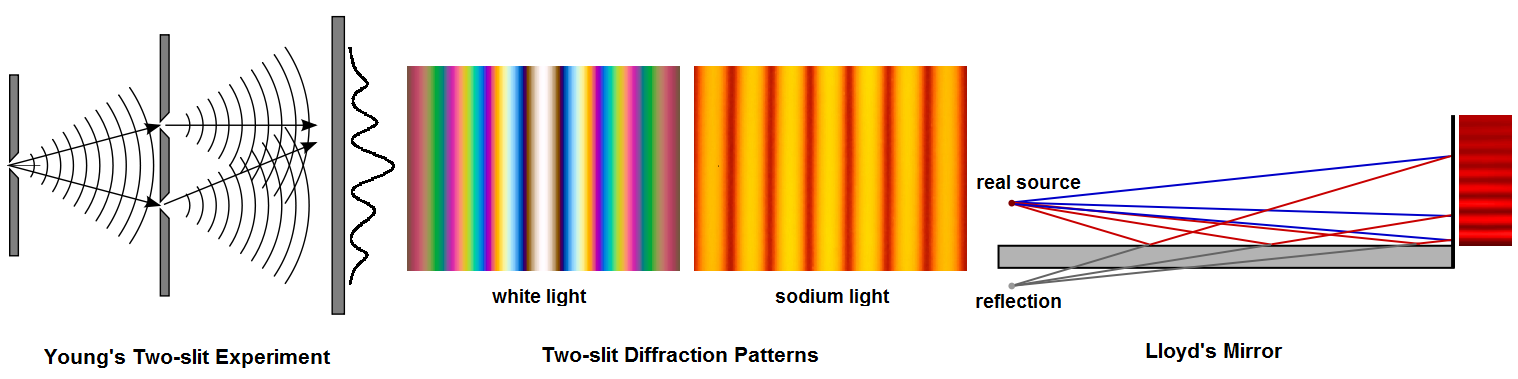
7.5.1 Experimento de la doble rendija
Cuando se superponen dos luces cualesquiera como, por ejemplo, las que provienen de dos bombillas, no nos es posible ver interferencias porque no son coherentes. Pero, desde esta idea surge una pregunta ¿Cómo se consiguen dos focos de luz coherentes? La solución la propuso Thomas Young en su famoso experimento de la doble rendija.
|
|
|
Imagen (adaptada) de Stigmatella aurantiaca en Wikimedia. CC |
La idea es muy simple: Hacemos incidir una luz monocromática (de una sola longitud de onda) por una doble rendija. Cada rendija actuará como si fuera una fuente de luz idéntica a la anterior, por lo que el resultado es que se tienen dos luces idénticas superponiéndose como se ve en la figura. Al ser ambas ondas idénticas, su diferencia de fase sólo depende del lugar en el que se superponen estas luces, obteniéndose una sucesión de máximos y mínimos de intensidad.
Tal como se ha visto en el tema Propiedades de las ondas, los máximos se repiten simétricamente en los lugares en los que la diferencia de caminos recorridos por las ondas desde las ranuras hasta el punto es igual a un número entero de longitudes de onda.
|
|
Con operaciones matemáticas se obtiene una fórmula que nos permite saber dónde están los máximos de intensidad.
La condición anterior significa que un punto de la pantalla estará iluminado si en él se cumple:
![]()
y estará oscuro en los puntos en los que se cumpla la condición:
![]()
Por otra parte, de la figura se deduce
![]()
Si se supone que D>>d, se cumple que senα≈tgα=y/D
Por lo tanto, la condición de máximo de intensidad se cumple en los puntos:
![]()
Dando valores sucesivos a n obtenemos los diferentes máximos de intensidad que se observan. Es, por ello, posible utilizar la expresión anterior para medir experimentalmente la longitud de onda, basta con conocer la distancia d entre rendijas y la distancia D a la pantalla.
Visualiza a continuación la simulación del proceso de interferencia por una doble rendija. Verás qué sucede al modificar la longitud de onda de las luces que se superponen.
|
Grabación de animación en Galileo and Einstein de Jacquie Hui Wan Ching bajo licencia C |