2.2. Aproximación y errores
 |
| Fotografía de tarostatic en Flickr. Licencia CC |
Aproximación
Si lo piensas bien, existen muchas situaciones en nuestra vida cotidiana donde utilizamos los números de manera aproximada:
- Cuando vamos a comprar frutas o verduras y pedimos un kilo o tres cuartos de algún producto, si nos fijamos bien en la cantidad que marca la balanza, casi nunca el frutero coloca la cantidad exacta de la mercancía que hemos solicitado. "Pasa un poco del kilo", nos dice el comerciante; o "le faltan 35 gramos para los tres cuartos".
- "Nos vemos a las siete y media en la puerta del cine", y nadie llega a la hora exacta a la cita. Muy pocos llegarán unos minutos antes, y casi todo el mundo con algo de retraso.
Que los números reales se expresen en el sistema decimal mediante expresiones decimales finitas o infinitas plantea problemas no menores de cálculo. ¿Cómo manejar expresiones decimales infinitas de las que no conocemos todas sus cifras? ¿Cómo manejar de forma aceptable números decimales con un número grande de cifras? Tales consideraciones llevan a los conceptos de aproximación y error.
Importante
Si en un número decimal, a partir de un determinado orden, sustituimos todas las cifras de orden inferior por ceros, obtendremos otro número decimal que se dice una aproximación del primero (hasta el orden fijado).
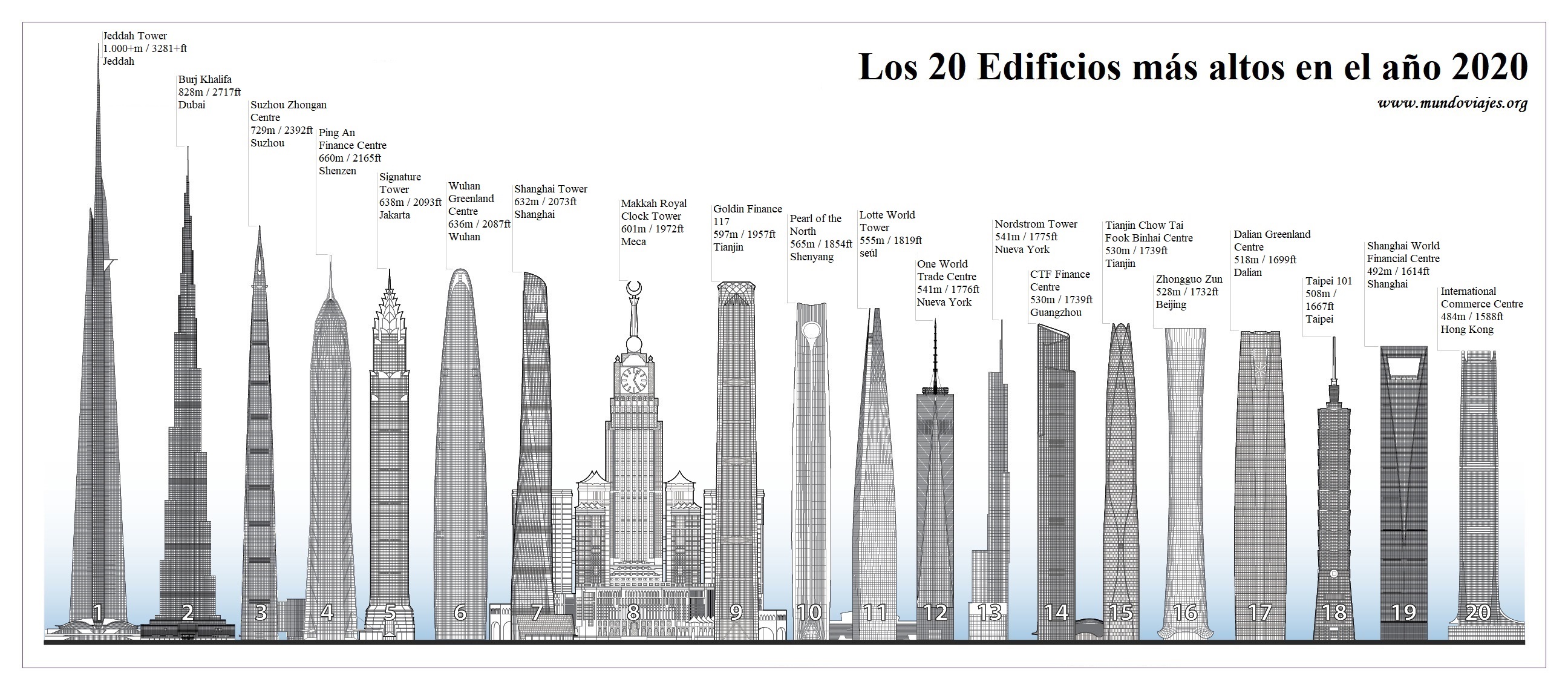
La siguiente imagen está tomada de una infografía de Mundo Viajes, (pulsa en la imagen para verla completa) en los que se comparan los edificios más altos del mundo en el 2020.
Te planteamos la siguiente reflexión, ¿crees que todos estos edificios miden exactamente los valores recogidos aquí? ¿No variará ni un centímetro? ¿Tendría sentido recoger en esta infografía los posibles decimales? La respuesta probablemente sea no, ya que las diferencias entre unos y otros son de metros.
Esto puede llevarnos a otro planteamiento... ¿existe un orden de aproximación establecido de antemano para hacer una aproximación? La respuesta es NO. Dependerá de lo que se desea medir. Así, carecería de sentido fijar el mismo orden de aproximación para medir la distancia entre dos ciudades o el diámetro de una pelota de tenis de mesa.
En el día a día no es necesaria mucha precisión, basta con 2 ó 3 decimales. Eso sí, la cosa cambia si manejamos datos científicos.
Hay distintos métodos de aproximación:
 |
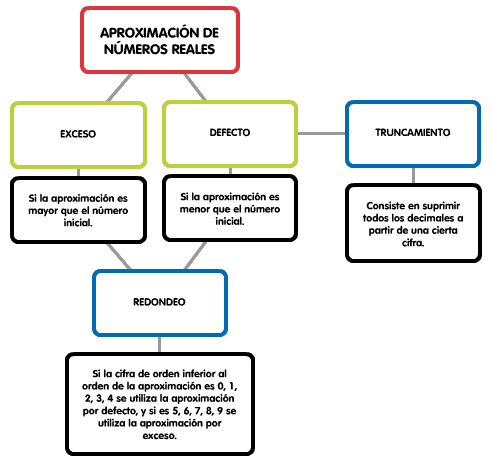| Imagen de elaboración propia |
Si te paras a pensar, hay veces que aproximamos por exceso y por defecto, sin darnos cuentas. Por ejemplo, la duración del año solar medio no contiene un número exacto de días. Se usan dos tipos de años: el de 365 días (aproximación por defecto) y el de 366 (año bisiesto, aproximación por exceso).
Importante
Se llaman cifras significativas a aquellas con las que se expresa un número aproximado. Solo debemos utilizar aquellas cuya exactitud nos conste.
Comprueba lo aprendido
Recordemos las diez primeras cifras decimales de nuestro querido número de oro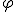 
=
1,6180339887.
Completa en la siguiente tabla los espacios en blanco correspondiente a las aproximaciones de 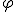que se indican.
Errores
Al sustituir un valor por su aproximación evidentemente se comete un error.
 |
En este reportaje al central del Valencia Marius Stankevicius, en la semana que se enfrentaban al Real Madrid, comentaba:
"El peor momento para un defensa es cuando tu equipo ataca: todos piensan en atacar y tú debes pensar en defender". Y la otra: "10 centímetros de error en el fútbol actual es suficiente. Te matan. No hace falta que el error sea grave".
Pero... ¿cuándo un error empieza a ser grave?
Caso práctico
 |
| Imagen de OpenClipart-Vectors en Pixabay. Licencia CC |
Veamos un caso práctico. En el prospecto de unas cápsulas se indica que cada gramo del medicamento contiene 0,00285 gramos de ácido bórico y 0,00015 gramos de tetraborato de sodio.
En un control de calidad farmacéutico, se toma una muestra de una de las cápsulas y se detecta que cada gramo de la medicina contiene 0,0031 gramos de ácido bórico y 0,00013 gramos de tetraborato.
- En uno de los casos el error es por exceso, supera a la cantidad fijada, y en el otro es por defecto, está por debajo. ¿cuál es uno y cuál es el otro?
- ¿En cuál de los dos componentes la diferencia entre la cantidad indicada en el prospecto y la detectada en el tubo es mayor?
Importante
Se denomina error absoluto a la diferencia entre el valor real de un número y su aproximación. Se suele tomar el valor absoluto de dicha diferencia.
Error absoluto =|valor real - aproximación|
Los errores absolutos cometidos en las muestras detectadas de la pomada son 0,000250 para el ácido bórico y 0,00002 en el tetraborato.
 |
| Noticia en ABC.es (26/05/2011) |
Observa la siguiente noticia:
Efectivamente, es un error muy grande pues había más votos que votantes.
Ignoramos si eran 10, 15 o 20, pero... ¿qué hubiera ocurrido si en vez de ser unas elecciones municipales hubieran sido unas autonómicas o unas generales? ¿Crees que habría salido en los periódicos? ¿Estaríamos hablando de error?
La respuesta a estas preguntas podría ser que el error es relativo dependiendo de la proporción de equivocación que haya en el total.
No es lo mismo una equivocación de 10 papeletas en 1.000 habitantes que de 10 papeletas en 35 millones.
Importante
Se define error relativo de una aproximación a un número como el cociente entre el error absoluto y el valor del número. El error relativo se puede expresar en tanto por uno o en tanto por ciento.
Observa la diferencia entre el error absoluto y el error relativo:
- Si hablamos de error absoluto siempre podemos indicar las unidades. Por ejemplo, hay 100 papeletas erróneas.
- Si lo hacemos en términos de error relativo la cosa cambia. Hacemos referencia al total, dando el resultado en porcentajes. Por ejemplo, un 1% de las papeletas son erróneas.
Comprueba lo aprendido
Solución
Solución
Caso práctico
Para vallar mi cortijo de Níjar (Almería) estimé que necesitaba 400 metros. Cuando la empresa VALLAS INDALO me la instaló cobraron 401 metros, cabe pensar que con mi cinta métrica de casa cometiera un error de 1 metro.
Cuando se lo comenté a mi vecino Pablo, que trabaja en la empresa CARRETERAS RURALES S.A, me explicó que a su encargado le había pasado algo parecido en la carretera que une los pueblos de Macael y Olula del Río (3 km de distancia). Con sus aparatos de medida cometieron el mismo error, 1 metro.
Para ambos casos el error de medición es de 1 metro.
¿Pero es distinta la significación de un error de un metro al medir 3 km que al medir 401 metros?
Curiosidad
Aproximaciones de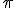 
La Tierra donde vivimos, la Luna que gira a nuestro alrededor, el balón alrededor del que giran la mirada y el ocio de millones de aficionados en todo el mundo y multitud de objetos tanto de la naturaleza como creados por el ser humano tienen forma esférica o, utilizando un lenguaje coloquial, son redondos. La rueda, sin duda uno de los grandes inventos de la humanidad, es una circunferencia. El uso de la rueda para el transporte, para girar en las norias y elevar el agua o batir las semillas en los molinos. No nos puede extrañar que desde muy pronto el ser humano se fijara en la circunferencia y se preguntara por la relación que existe entre el perímetro y el diámetro. De esa relación surgió uno de los números más famosos y conocidos por todas las civilizaciones: 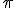. Para convencerte de que es cierto lo que hemos dicho, disfruta de este vídeo:
Vídeo de Belén Sepúlveda alojado en Youtube