2.1. Intervalos y semirrectas
Intervalos
Observa la siguiente imagen, referida a la calificación de las películas según su contenido y su adecuación al público según la edad.
Imagen de elaboracion propia
Si te fijas, no hablamos de que un determinado film es apto para personas de exactamente 12 años, sino para personas mayores de o menores de. Dicho de otra forma, la cinta no está recomendada para personas menores de 12 años, o para edades comprendidas de los 0 a los 12.
Importante
Si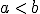 
se llama intervalo de extremos 
y 
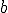al conjunto de números que están entre y 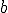en la relación de orden. Según contengan o no los extremos los intervalos se llaman cerrados, abiertos o semicerrados o semiabiertos si contienen solamente uno de los extremos.
Es decir, los intervalos son "trozos" de la recta real.
 |
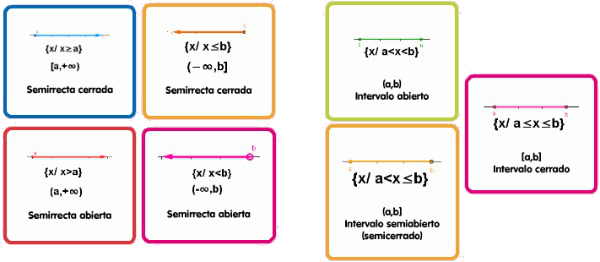| Imagen de elaboración propia |
Si observas la imagen anterior, tenemos distintas formas de expresar un intervalo:
-
- Gráficamente: utilizando la recta real, e indicando los extremos del intervalo.
-
- A través de conjunto y desigualdades
- Notación de intervalo. En este caso observa que en el caso de las semirrectas, el infinito nunca está contenido.
- A través de conjunto y desigualdades
En el siguiente vídeo, puedes ver los diferentes tipos.
Vídeo de Tuto mate alojado en Youtube.
Ejercicio resuelto
Escribe como intervalo los siguientes conjuntos de números reales:
a) Los números que están entre 3 y 10:
b) Los números mayores que 0 y menores o iguales que 8.5:
c) Los números menores que 2/3:
Comprueba lo aprendido
 |
| Imagen de elaboración propia |
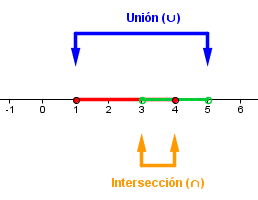
Al igual que operábamos con números, con los intervalos podemos hacer algunas operaciones:
- Unión (U): al unir dos intervalos, consideramos los números que están en uno u otro intervalo:
[1,4] U (3,5) = [1,5)
- Intersección (∩): la intersección de dos intervalos consiste en quedarse con los números que están en los dos a la vez:
[1,4] ∩ (3,5) = (3,4]
En los siguientes vídeos, puedes ver la unión y la intersección.