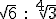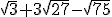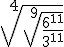1.3. Radicales. Operaciones
Hemos llegado a uno de los apartados más importantes del tema: la noción y el manejo de radicales.
Su importancia para nosotros no sólo se debe al papel que jugaron en el descubrimiento de los números irracionales, sino también por la frecuencia con que aparecen en la prueba que estamos preparando.
Ya hemos estudiado en el tema anterior operaciones como la suma, y la multiplicación, así como sus inversas, la resta y la división. Pero no podemos dejarnos en el tintero la potenciación. Observa el siguiente cuadro:
| Potenciación | Radicación |
|---|---|
|
Conocemos la base, 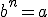 |
Conocemos la potencia, |
La radicación es una operación relacionada con la potenciación, y se representa utilizando el símbolo √ que proviene de la inicial de la palabra en latín, radix. En muchas ocasiones da como resultado un número irracional (recuerda que la raíz cuadrada de 2 fue posiblemente el primer número irracional conocido).
Importante
Una potencia de exponente fraccionario 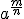 es un radical de índice
es un radical de índice 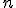 y radicando
y radicando 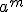 , y se denota por:
, y se denota por: 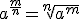
Importante
Decimos que la raíz n-ésima de un número  es
es 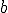 si cumple que
si cumple que 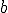 elevado a
elevado a 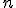 es
es  . Es decir:
. Es decir:
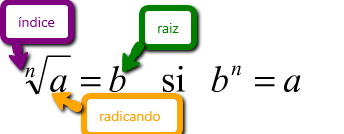
Imagen de elaboración propia.
Comprueba lo aprendido
Simplificar radicales
Simplificar un radical es escribirlo en la forma más sencilla, de manera que:
- El índice y el exponente sean primos entre sí.
- No se pueda extraer ningún factor del radicando.
- El radicando no tenga ninguna fracción.
Veamos en un vídeo cómo hacerlo:
Vídeo de Tuto mate alojado en Youtube
Comprueba lo aprendido
En la siguiente escena del proyecto edad puedes practicar con la simplificación de radicales:
Escena de Miguel Angel Cabezón Ochoa en Proyecto Descartes. Licencia CC
Suma y resta de radicales
En el siguiente vídeo puedes ver cómo sumar radicales:
Vídeo de Tuto mate alojado en Youtube
Comprueba lo aprendido
En la siguiente escena del proyecto edad puedes practicar con la suma y resta de radicales:
Escena de Miguel Angel Cabezón Ochoa en Proyecto Descartes. Licencia CC
Producto y división de radicales
Para multiplicar radicales o dividir radicales se necesita que tengan el mismo índice, cuando esto ocurre el resultado:
- De la multiplicación es un radical del mismo índice y de radicando el producto de los radicandos.
- De la división es un radical con el mismo índice y radicando el cociente de los radicandos.
Vídeo de Tuto mate alojado en Youtube
Ejercicio resuelto
Opera y simplifica:
Ejercicio resuelto
- Pasa a radicales con índice común las raíces
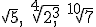 .
.
- Pasa a radicales con índice común, y ordena de menor a mayor, las raíces
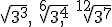
- Calcula
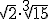
- Calcula