1.1. De los irracionales a los reales
 |
| Fotografía en Pxhere. Licencia CC |
Ya los antiguos griegos descubrieron que había objetos, cuyas dimensiones no podían expresarse con los números racionales, una vez elegida una unidad. Llamaron a tales magnitudes inconmensurables, que no pueden medirse.
La unión del sustantivo ‘magnitudes’ y el atributo ‘inconmensurables’ parece encerrar en sí misma una contradicción o paradoja. Constituyen el equivalente en lenguaje geométrico de lo que en lenguaje numérico se designa hoy día como número irracional.
Un número irracional, contra lo que puede parece a simple vista, no es un número absurdo, ilógico, sino un número que no es racional, que no puede expresarse como cociente de números enteros.
Importante
El conjunto de los irracionales, I, está formado por los números que no pueden ser expresados como fracción. Su expresión decimal tiene un número infinito de cifras que no se repiten de forma periódica.
Existen infinitos números irracionales. Algunos de ellos, por su importancia histórica y práctica, han llegado a adquirir un nombre propio.
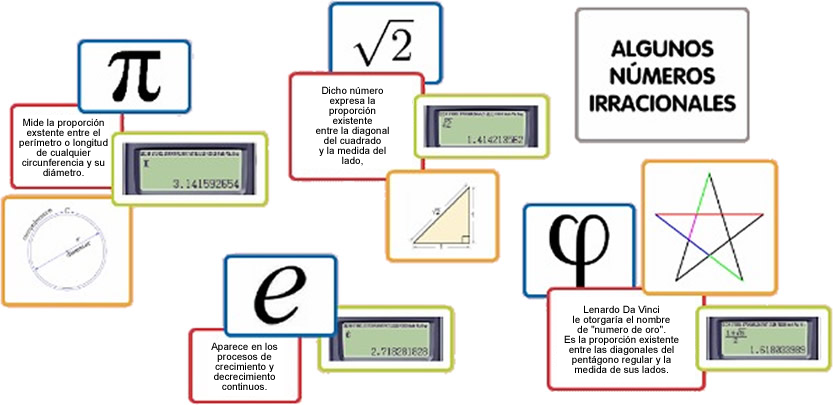
Imagen de elaboración propia.
¿Cómo escribir los números irracionales?
Si te fijas en la imagen anterior, el número de oro o número áureo phi (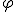
o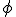 
), viene expresado a través de una suma y un cociente de un número irracional 
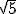, con dos números racionales, pues bien, la irracionalidad de phi, no es casualidad.
Importante
Si a un número irracional le sumamos (restamos) o lo multiplicamos (dividimos) por un número racional, el resultado es un número irracional.
Según el importante anterior, en algunos casos podremos escribirlos de forma simbólica, basándonos en otros números irracionales. Pero en el caso en el que recurramos a su expresión decimal, escribimos el número hasta una determinada cifra e indicamos mediante puntos suspensivos que los decimales continúan. Esto nos permitirá no confundirlos con números decimales exactos.
Los números reales
Importante
Se llama número real a cualquier expresión decimal, ya tenga una cantidad finita o infinita de cifras.
El conjunto de los números reales se denota por 
.
Se clasifican en:
- Racionales (pueden expresarse como cociente de números enteros)
- Irracionales (no racionales)
El conjunto de los números reales se puede representar como si de un cuadro de Mondrian se tratara: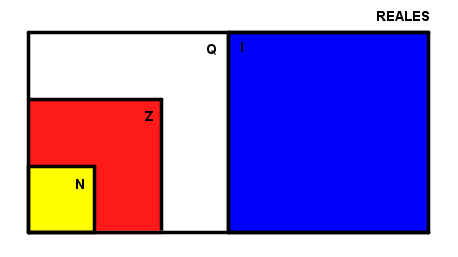
Imagen de elaboración propia.
Si te fijas, uno de los aspectos más sorprendentes de la historia de los números es que cada nueva invención es ampliación de las precedentes y, de alguna manera, las completa. Los números enteros incluyen los naturales, los números racionales incluyen los números enteros y los reales incluyen los racionales y los irracionales. En el siguiente vídeo puedes verlo con más claridad, además de practicar con algunos ejemplos de clasificación de números.
Vídeo de Tuto mate alojado en Youtube.
Aunque parezca increíble la historia de los números no termina con los números reales. Existe otro conjunto de números llamado números complejos que, como no podía ser de otra forma, está repleto de números imaginarios.
Comprueba lo aprendido
Retroalimentación
Falso
Ten en cuenta que es la raíz cuadrada de un número natural que no es cuadrado perfecto.Retroalimentación
Verdadero
Fíjate bien, es una fracción de dos números enteros.Retroalimentación
Falso
Observa que es un número decimal con infinitas cifras periódicas.Retroalimentación
Verdadero
Los reales son todos los racionales e irracionales.Curiosidad
Sobre el nombre de irracional
Los nombres de racionales e irracionales viene de las matemáticas griegas.
Racional tiene su origen en razón, que no tiene otro sentido mas que proporción o división. Un número racional es el que se puede expresar como proporción de dos números enteros. Por tanto, un irracional es el número que no se puede escribir como el cociente de dos enteros.
Para entender mejor la diferencia entre racionales e irracionales, veamos la imagen que propone el profesor Fernando Corbalán: "si asignamos un sonido a cada cifra y hacemos sonar los decimales de un racional, escucharíamos una melodía que se va repitiendo, como el estribillo de una canción. En el caso de los números irracionales las notas sonarían sin ton ni son, y no podríamos obtener jamás una melodía".