5. Carácter no conservativo del campo magnético
En anteriores temas has estudiado que los campos gravitatorio y eléctrico son campos conservativos. ¿Qué ocurrirá con el campo magnético? Veámoslo.
Sabemos que un campo es conservativo cuando el trabajo entre dos puntos cualesquiera no depende del camino recorrido. En la siguiente animación hemos representado cuánto vale el trabajo en el seno del campo eléctrico creado por una carga Q. Se puede observar que el trabajo para desplazar la carga q desde el punto A hasta el punto B es el mismo pasando por A' o por B'.
| Animación de Antonio González en Geogebratube |
Esto es equivalente a decir que el trabajo en cualquier trayectoria cerrada es nulo.
| Animación de Antonio González en Geogebratube |
A lo largo del camino cerrado, el trabajo se anula en los tramos A'B y B'A porque la carga q se mueve en dirección perpendicular al campo y a la fuerza eléctrica. En los tramos AA' y B'B el trabajo realizado es el mismo pero cambiado de signo. En el primer caso la carga q se mueve en contra del campo eléctrico y en el segundo a favor. Por lo tanto el trabajo total es nulo.
| Animación de Antonio González en Geogebratube |
Matemáticamente, la condición para determinar si un campo es conservativo o no es que su circulación a lo largo de un camino cerrado sea nulo.
| Animación de Antonio González en Geogebratube |
Vamos a calcular la circulación a lo largo de un camino cerrado en un campo magnético. Lo haremos en un caso sencillo que ya hemos estudiado: el campo magnético creado por un conductor rectilíneo indefinido que conduce una intensidad de corriente I.
 |
| Imagen de elaboración propia |
Sabemos que este hilo genera un campo de módulo:
![]()
Las líneas de campo son circunferencias centradas en el hilo conductor en planos perpendiculares a este. Nos centramos en el plano z=0 y más concretamente en una de las líneas de campo.
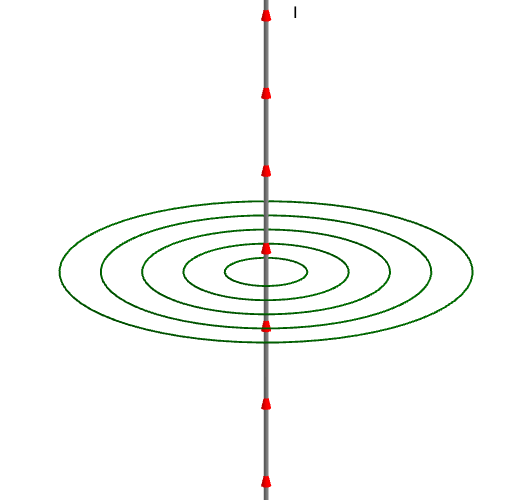 |
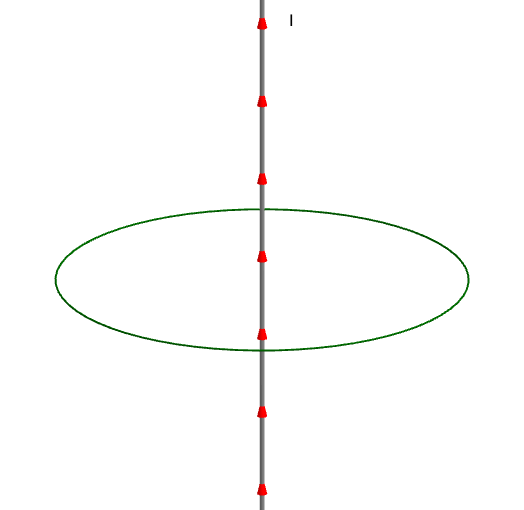 |
| Imágenes de elaboración propia | |
El campo magnético, según la regla de la mano derecha, tendrá dirección tangente a la línea de campo y sentido antihorario. En cualquier punto de la circunferencia, el módulo del campo magnético es el mismo, su dirección tangente a la curva y siempre con sentido antihorario.
 |
| Imagen de elaboración propia |
Calculemos la circulación del campo magnético a lo largo de la circunferencia.
![]()
Un trozo infinitesimal de recorrido se obtendría dividiendo la circunferencia en trozos cada vez más pequeños. Si lo hiciéramos ese trozo de camino sería tangente a la circunferencia.
| Animación de Antonio González en Geogebratube |
Pregunta Verdadero-Falso
Indica qué afirmaciones son verdaderas y cuáles son falsas.
Retroalimentación
Falso
Retroalimentación
Falso