3.3. Buscando solución a los problemas diarios
 |
|
Planet, de Southernpixel, |
¿Sirven las ecuaciones en el mundo que nos rodea?
Ya sea consciente o inconscientemente, resolvemos problemas del día a día por medio de ecuaciones: al comparar productos en el mercado, cuando hacemos viajes, en nuestras cuentas bancarias y al buscar una nueva compañía telefónica. Incluso para hacer la foto de la izquierda, se han usado ecuaciones.
Vamos a ver algunos tipos de problemas que se resuelven con ecuaciones de primer o segundo grado con una incógnita. Evidentemente no todos los problemas tienen solución, ni todos los podemos solucionar con las herramientas que tenemos hasta este momento, pero ya verás que tan sólo con lo que hemos visto, ya se pueden resolver bastantes situaciones.
Ejemplo o ejercicio resuelto
En mi compañía telefónica me ofrecen una tarifa reducida y una tarifa plana para el móvil. Las condiciones de cada una son las siguientes:
| Concepto |
Tarifa Reducida |
Tarifa Plana |
|
Establecimiento
|
15 cént. | 15 cént. |
|
Llamadas a móviles
|
3 cént./min. | 19,9€/mes |
|
Llamadas a móviles
|
30 cént./min | 18 cént./min |
Mirando las facturas de los últimos meses, he visto que suelo hablar el doble de tiempo con los móviles de mi compañía que con los que son de otra. ¿Cuánto tiempo tengo que hablar para que las dos tarifas me salgan por el mismo precio?
Como el establecimiento de llamada es el mismo en las dos tarifas, y podemos suponer que haré el mismo número de llamadas con ambas, no vamos a considerar este dato. Ten en cuenta que todos los valores los pasaremos a euros. Vamos a plantear el problema paso a paso:
a) Si x es el número de minutos que hablo al mes con los móviles de otras compañías, ¿cuánto me gastaré al cabo de un mes con la tarifa reducida?
AV - Actividad de Espacios en Blanco
AV - Actividad de Espacios en Blanco
AV - Actividad de Espacios en Blanco
 |
| Fotografía de Missy Schmidt en Flickr. Licencia, CC |
En Física, el espacio que recorre un cuerpo que se mueve en linea recta sin variar la velocidad, viene dado por la fórmula e = e0+vt, donde t es el tiempo y e0 es el espacio inicial.
Si en ese movimiento lo que permanece constante es la aceleración, entonces tenemos 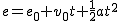 , donde v0 es la velocidad inicial, a es la aceleración y t el tiempo.
, donde v0 es la velocidad inicial, a es la aceleración y t el tiempo.
En este vídeo puedes ver la resolución de algunas problemas.
Para saber más
Para que puedas practicar los conceptos y procedimientos explicados en el tema te proponemos que visites el siguiente enlace, donde encontrarás gran cantidad de ejercicios resueltos.
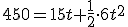
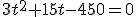
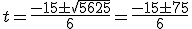
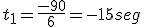 (no es válida por ser un tiempo negativo)
(no es válida por ser un tiempo negativo)