3.1. Estudio de la Correlación
 |
| Fotografía en Flickr de Kevin Dooley bajo CC |
¿Recuerdas las nubes de puntos del apartado anterior? Con ellas podíamos determinar si había algún tipo de relación o dependencia entre dos variables, y en ese caso decidir si la relación era positiva o negativa (al aumentar la primera, aumentaba o disminuía respectivamente la segunda).
Esta relación la definiremos como correlación. Y esta puede ser:
- Correlación funcional: si existe una relación funcional entre las variables X e Y. Es decir, podemos calcular los valores de Y a partir de los de X, con una función.
- Correlación positiva o directa: existe cierta relación entre ambas variables, y al aumentar los valores de X también aumentan los de Y.
- Correlación negativa o inversa: existe cierta relación entre las variables, pero al aumentar los valores de X disminuyen los de Y.
- Correlación nula: no existe ningún tipo de relación entre ambas.
Observa ahora las dos siguientes gráficas obtenidas al hacer el mismo estudio sobre dos poblaciones diferentes.
 |
 |
Como puedes ver, en ambas la correlación es positiva. Pero, ¿crees que en los dos casos existe la misma dependencia entre las variables? Por lo que se puede apreciar en las gráficas, en el Estudio A la dependencia parece ser más fuerte que en el Estudio B. Por tanto, debe existir alguna forma para medir la correlación.
A continuación, definiremos dos parámetros, la covarianza y el coeficiente de correlación lineal, que nos servirán para establecer esta medida.
Al igual que teníamos en el tema anterior medidas que nos ayudaban a interpretar los datos de una distribución unidimensional, en las bidimensionales tenemos la covarianza, que nos permite saber si la relación entre las variables es directa o inversa, y si dicha relación puede ser lineal o no.
Importante
La covarianza de una variable bidimensional (X,Y), que representaremos por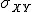 
, es una medida estadística que se calcula usando una de las expresiones:
| Tablas simples |
Tablas de doble entrada |
 |
 |
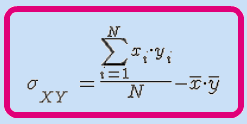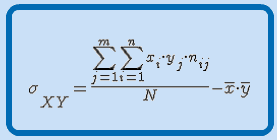donde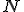 
indica el tamaño de la muestra.
Interpretación: el signo de la covarianza nos permitirá saber el tipo de correlación:
- Si la covarianza es positiva, la correlación será directa.
- Si la covarianza es negativa, la correlación será inversa.
En la siguiente presentación puedes ver cómo calcularemos la covarianza a partir de una tabla simple.
Presentación en Slideshare de Saúl Valverde
Ejemplo o ejercicio resuelto
En un estudio sociológico se está analizando el nivel de estudios de la población y el salario mensual de estos. Los datos obtenidos se reflejan en esta tabla:
| Nivel de estudios |
1 | 2 |
3 |
4 |
5 |
| Salario medio (€) |
700 |
940 |
1.120 |
1.300 |
2.180 |
donde 1=Sin titulación, 2=Estudios secundarios, 3=Técnicos de grado medio, 4= Bachillerato y 5=Técnicos superiores o licenciados.
¿Cuál es el valor de la covarianza?
A la salida de un restaurante se hace una encuesta en la que se pregunta el número de persona que vienen a comer juntas, X, y la calificación de 1 a 4 que le pondrían al restaurante, Y. Los datos recogidos se han ordenado en la tabla:
| X \ Y |
1 |
2 |
3 |
4 |
| 1 | 0 | 1 | 0 |
0 |
| 2 | 2 | 3 | 4 |
1 |
| 3 | 2 | 3 | 6 | 1 |
| 4 | 0 | 0 | 2 |
0 |
¿Cuál es la covarianza?
Coeficiente de correlación lineal
También llamado coeficiente de correlación de Pearson es el parámetro que nos va a decir si la correlación es débil o fuerte, además de indicarnos también si es directa o inversa dependiendo de su signo.
Importante
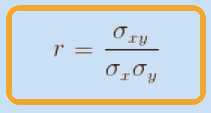
siempre será un número comprendido entre -1 y 1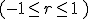 
. Su signo nos indicará el sentido de la correlación (positiva o negativa) y mientras más próximo esté su valor a 1 o -1, más fuerte será la correlación.
Interpretación: Según el valor de r, la correlación entre las dos variables será:
- r = 0: No existe correlación (correlación nula).
- r = 1 : La correlación es perfecta y positiva (correlación funcional positiva).
- r = -1: La correlación es perfecta y negativa (correlación funcional negativa).
- r próximo a 1: La correlación es fuerte y positiva.
- r próximo a -1: La correlación es fuerte pero negativa.
- r próximo a 0: La correlación es débil.
Veamos cómo calcularla con el ejemplo anterior.
