2.2. Gráficas y nubes de puntos

|
| Fotografía en Flickr de Ian Sane bajo CC |
Representación de datos
Si te fijas en los pasos que hemos dado hasta este momento, verás que es un proceso muy lógico:
- Nos planteamos una pregunta sobre la relación entre dos parámetros.
- Tomamos suficientes datos de ambos parámetros sobre la población que nos interesa.
- Organizamos estos datos en una tabla simple o de doble entrada.
El siguiente paso será visualizar estos datos en una gráfica, de modo que nos resulte más fácil dar respuesta a nuestra pregunta inicial.
CASO I: Datos ordenados en una tabla de doble entrada
Como este caso no lo vamos a trabajar, te recomendamos que visites el apartado de Curiosidades en el apéndice si quieres saber algo más sobre esta cuestión. Eso sí, te adelantamos que se hablarán de Histogramas tridimensionales y Diagramas de dispersión o de burbujas.
CASO II: Datos recogidos en una tabla simple
Este es el caso sobre el que vamos a trabajar. Además, la representación te resultará familiar de la unidad 2, ya que tenemos unos ejes cartesianos y puntos con dos coordenadas x e y.
Por ejemplo: vamos a representar los valores de Temperatura y Precipitaciones medias mensuales en una determinada estación climatológica que tenías en la autoevaluación del apartado anterior.
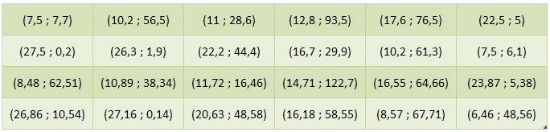
|
Diagrama de dispersión o Nube de puntos:
Al igual que el Diagrama de Burbujas, se representa sobre un par de ejes cartesianos. En este caso, cada punto representa un par de datos de la Variable Estadística Bidimensional.
|
|
Dependencia
Las Nubes de Puntos también nos ayudan a ver la dependencia entre las variables. Si recuerdas, en el primer apartado vimos que la dependencia podía ser:
- Dependencia positiva: Al aumentar la variable X, también aumenta la Y.
- Dependencia negativa: Al aumentar la variable X, disminuye la Y.
- Sin dependencia: No se observa ninguna relación entre las dos variables.
- Dependencia funcional: Podemos encontrar una relación exacta entre ambas variables que siempre se cumple. Por ejemplo, si estudias la relación entre el número de cajas de leche y el número de litros que se compra de una marca, tenemos una dependencia funcional, porque cada caja tiene siempre el mismo número de litros. Puede ser más o menos fuerte dependiendo de que el diagrama de dispersión tienda a acercarse más o menos a la representación de la función. Nos interesará conocer si es positiva o negativa, así como si es lineal o curvilínea.
- Dependencia aleatoria: No hay una regla exacta que determine la relación entre ambas variables, como en el ejemplo anterior.
Mira las siguientes gráficas correspondientes a diferentes ejemplos. Verás que es mucho más fácil ver así la dependencia:
| |
|
| Dependencia positiva aleatoria |
Dependencia positiva funcional |
| Sin dependencia |
Dependencia negativa aleatoria |