4. Interferencias
Ya se ha hablado de la posibilidad de obtener cualquier onda por medio de la combinación de distintas ondas armónicas.
Pero, Bernoulli fue algo más allá. Propuso el principio de superposición de ondas, para el caso en que dos o más movimientos ondulatorios procedentes de distintos focos y propagándose en el mismo medio se encontrasen.
Se habla de interferencia cuando dos ondas llegan a un mismo punto de forma simultánea y se produce una alteración de las mismas. Dicha nueva perturbación viene a ser la suma de las ondas que coinciden en ese punto. Después de interferir, las ondas no sufren modificaciones y siguen propagándose con la misma dirección y sentido que tenían antes de encontrarse, como si hubiesen sido independientes. Este hecho es una característica de las ondas que las hace tan diferentes de los cuerpos materiales, que no pueden superponerse en un punto del espacio, curiosamente, en posteriores temas podrás ver que no es tan evidente la diferencia entre ondas y materia.
Así mismo, Bernoulli dedujo que la elongación a la que está sometido un punto es igual a la suma vectorial de las elongaciones producidas por cada movimiento por separado. Existiendo dos posibilidades: refuerzo de la onda o anulación de la misma. Para la primera situación se habla de interferencia constructiva y para el otro interferencia destructiva.
A continuación, se muestra una simulación que comenzará a clarear el asunto.
El caso más simple lo constituye la interferencia de dos ondas de la misma frecuencia procedentes de dos focos sincronizados (es decir, que están en concordancia de fase o cuyas fases mantienen una diferencia constante). Las llamamos ondas coherentes.
Sea pues las siguientes ondas:
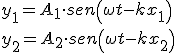
Observa que la diferencia de fase entre ambas es δ=k(x2-x1)
La suma de ambas, usando los conocimientos de trigonometría, da lugar a:
![]()
![]()
Te recuerdo que:
![]()
por lo que, siempre que las ondas tengan la misma amplitud
Concluimos:
![]()
Otra posibilidad:
![]()
El primer término representa la amplitud de un a onda que, como ves, depende de la diferencia de fase (de ahí que sea importante, para observar la interferencia, que la diferencia de fase sea constante)
Como ves, la expresión tiene dos partes. Una tiene una componente seno que se puede decir que representa a un movimiento armónico simple y el segundo factor dará cuenta del desplazamiento con respecto a la posición de equilibrio.