1. Estimación puntual
¿Qué tal llevas el curso?
En el tema anterior aprendiste a elegir correctamente una muestra representativa de una población para estudiar alguna característica de ella, en el siguiente te vamos a enseñar como analizar los datos obtenidos y observar si estos valores se encuentran en unos determinados intervalos a los cuales llamaremos "intervalos de confianza", además de eso llevarás un control del error que estas cometiendo en cada momento.
Todo esto lo estudiarás contando con la ayuda de la empresa TisBet Survey, especialista en realizar este tipo de estudios estadísticos.
A nuestros amigos de la empresa TisBet Survey les han encargado la Concejalía de Educación de su Ayuntamiento, un estudio sobre el Cociente Intelectual (C.I.) medio de los alumnos y alumnas del IES "Benito V.", ya que están elaborando un proyecto de atención a alumnado con altas capacidades.
Como no conocen la proporción de alumnos que tienen un C.I. superior a 130 (alta capacidad), toman una muestra aleatoria con alumnos y alumnas del instituto, a través de la cual calcularán una aproximación del número total de alumnos con alta capacidad en el Centro.
Esta aproximación es lo que llamamos estimación.
Junto a esta estimación, y dado que muy probablemente no coincida con el valor real del parámetro, acompañarán el error aproximado que se comete al realizarla.
¿Qué ocurre una vez calculado la proporción de alumnos en la muestra con C.I. superior a 130?
Supongamos que los trabajadores de TisBet Survey han seleccionado una muestra de 100 alumnos y alumnas y han obtenido que sólo 3 alumnos tienen un C.I. superior a 130, es decir, la proporción de alumnado con alta capacidad es del 3% (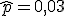
).
Parece lógico estimar que la proporción de todo el alumnado del instituto con alta capacidad será aproximadamente igual que la proporción de la muestra, 3%. Pero, ¿cómo de aproximadamente?
El hecho de decir que el valor de p es aproximadamente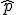 
, significa que estamos haciendo una estimación puntual.
Actividad
Una estimación puntual del valor de un parámetro poblacional desconocido (como puede ser la proporción p ), es un número que se utiliza para aproximar el verdadero valor de dicho parámetro poblacional.
A fin de realizar tal estimación, tomaremos una muestra de la población y calcularemos el parámetro muestral asociado (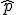 para la proporción).
El valor de este parámetro muestral será la estimación puntual del parámetro poblacional.
AV - Pregunta de Selección Múltiple
Solución
Solución
Solución
Actividad
Las estimaciones puntuales son más precisas que las estimaciones por intervalos que veremos en el siguiente apartado, sin embargo, son menos fiables que éstas.
¿Qué propiedades debe cumplir todo buen estimador?
- Insesgado: Un estimador es insesgado cuando la proporción
de su distribución muestral asociada coincide con la proporción de la
población. Esto ocurre, por ejemplo, con el estimador 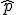ya que coincide con p.
- De varianza mínima: La variabilidad de un estimador viene determinada por el cuadrado de su desviación estándar. En el caso de 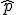el error estándar es
.
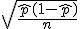Como puedes observar, cuanto mayor sea el tamaño de la muestra n, menor será la variabilidad del estimador 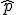, por tanto, mejor serán nuestras estimaciones.
La diferencia entre el verdadero valor del parámetro que se estima y el muestral mide el error cometido al utilizar el estimador y se denomina sesgo.
Cuando en un estimador la varianza es mínima, decimos que el estimador es eficiente.
Ejemplo o ejercicio resuelto
A la empresa TisBet Survey le han encargado una encuesta para saber la proporción de familias que utiliza cierto tipo de detergente.
Para ello ha seleccionado a 900 familias, calculando que la proporción estimada es 0,35.
¿Cuál es el error estándar estimado?
AV - Pregunta de Elección Múltiple
AV - Actividad de Espacios en Blanco
La empresa farmacéutica de nuestra localidad quiere hacer un estudio sobre la proporción de estudiantes de la Facultad de Matemáticas de la Universidad de Nogara que visitan al dentista al menos una vez al año.
Para ello, la empresa TisBet Survey escoge una muestra de 120 estudiantes, resultando que sólo 36 lo hacen.
Estima la proporción de estudiantes que visitan al dentista al menos una vez al año.