1.3 Funciones cuadráticas y otras polinómicas

Ejemplo:
El "Fórmula Uno" del apartado anterior mantenía la velocidad constante durante toda la recta. Esa situación es poco probable, en una recta tan larga los pilotos, como es lógico, suelen acelerar.
En la siguiente tabla se vuelven a relacionar el tiempo y la distancia a la que está el "F1" del inicio de la recta. Si la miras con detenimiento podrás ver que se empieza a cronometrar cuando el coche se encuentra a 66 metros del comienzo de dicho tramo. Además, cada segundo que pasa el espacio que recorre aumenta (no es constante como en el caso de las funciones lineales y afines). Este tipo de movimientos se denominan uniformemente acelerados.
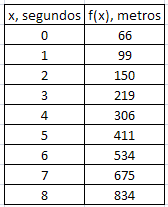
En la siguiente imagen se puede ver cómo es la gráfica de esta nueva función. Junto a ella aparece representada cómo van aumentando las distancias recorridas en cada tramo de 1 segundo de tiempo.

La expresión analítica de dicha función es 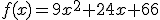 . Como puedes ver su fórmula es un polinomio de segundo grado y su gráfica una parábola. A las funciones de este tipo se las denomina cuadráticas.
. Como puedes ver su fórmula es un polinomio de segundo grado y su gráfica una parábola. A las funciones de este tipo se las denomina cuadráticas.
Importante
A las funciones cuya expresión algebraica es del tipo 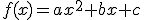 , donde
, donde  ,
, 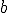 y
y  son números reales y
son números reales y 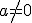 , se les denomina funciones cuadráticas.
, se les denomina funciones cuadráticas.
El dominio de cualquier función cuadrática son todos los números reales. La gráfica es una parábola con el eje de simetría paralelo al eje de ordenadas, y para saber el recorrido es necesario conocer el vértice de dicha parábola.
La parábola es una de las curvas clásicas de las matemáticas, las cónicas. Su silueta aparece en muchos procesos físicos como pueden ser el lanzamiento de objetos o el chorro del agua en las fuentes, también en el diseño de faros, antenas o cualquier otro cuerpo que emita o capte algún tipo de onda, y en obras de arte y arquitectura.

En la siguiente presentación se describe con claridad todo lo relativo a las funciones cuadráticas:
Comprueba lo aprendido
Una persona se encuentra situada en la terraza de un edificio, lanza una pelota hacia arriba. La función que relaciona los segundos que transcurren desde el lanzamiento con la altura, en metros, a la que se encuentra la pelota es 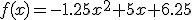 .
.
Ayúdate de lo que ya sabes de la función cuadrática y completa las siguientes frases.
En el siguiente vídeo, puedes ver cómo representar una función cuadrática:
Vídeo de tutomate alojado en Youtube
Ejercicio Resuelto
Representa la función 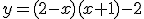 .
.
Caso práctico
Representa la función 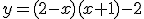 .
.
Para saber más
Aplicaciones de las funciones cuadráticas
Pinchando en la siguiente imagen puedes acceder a Proyecto Descartes y descubrir tres aplicaciones de las funciones cuadráticas:
Para saber más
Otras funciones polinómicas
Una función de la forma f(x)=anxn+an-1xn-1+...+a2x2+a1x+a0 donde n es un número natural, a0, a1, ... , an son números reales y an es distinto de cero, se llama función polinómica de grado n.
Sus características básicas son:
- El dominio de cualquier función polinómica es todo el conjunto de los números reales.
- El recorrido de una función polinómica de grado impar es todo el conjunto de los números reales.
- Siempre se pueden dibujar de un sólo trazo.
- Como máximo, cortan al eje OX en n puntos.
- Tienen, a lo sumo, n-1 máximos o mínimos relativos.
- Como máximo, tienen n-2 puntos de inflexión.
Presentación en Slideshare por saulvalper

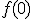 , ya que en el instante
, ya que en el instante 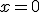 la pelota aun no ha sido lanzada. Y tenemos que
la pelota aun no ha sido lanzada. Y tenemos que 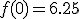 , que es el término
, que es el término  de la función cuadrática.
de la función cuadrática.
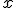 del vértice de la parábola. Para ello hacemos
del vértice de la parábola. Para ello hacemos 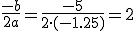 . Luego a los dos segundos.
. Luego a los dos segundos.
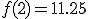 metros.
metros.
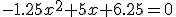 . Operando, obtenemos que las soluciones son -1 y 5. Pero -1 segundo no tiene sentido, luego la solución correcta será a los 5 segundos.
. Operando, obtenemos que las soluciones son -1 y 5. Pero -1 segundo no tiene sentido, luego la solución correcta será a los 5 segundos.