1.2 Funciones afines
Ejemplo:
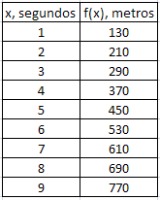
Volviendo a la recta de meta del circuito de Bahrein en Shakir, ahora nos interesa saber los metros que lleva recorrido desde el comienzo de la recta. El tramo en el que mantiene la velocidad constante de 80 metros por segundo está a 50 metros del inicio de dicha recta. Por tanto, la tabla y la gráfica de esta nueva función quedarían:
 |
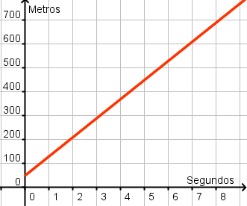 |
Como puedes observar, la tabla es parecida a la anterior, lo que ocurre es que se le ha sumado 50 a los metros recorridos en cada segundo. La gráfica continúa siendo una recta, pero 50 metros más alta que la gráfica anterior. ¿Cómo quedaría la expresión analítica?
La fórmula sería 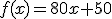 . Como puedes ver, esos 50 metros iniciales de la recta hay que tenerlos en cuenta en cualquiera de las formas de expresar esta nueva función.
. Como puedes ver, esos 50 metros iniciales de la recta hay que tenerlos en cuenta en cualquiera de las formas de expresar esta nueva función.
A una función con una expresión del tipo anterior, que tiene por gráfica una recta que no pasa por el origen de coordenadas, se le llama función afín.
Importante
A las funciones cuya expresión algebraica es de la forma 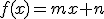 , con
, con 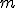 y
y 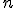 números reales, se les denomina funciones afines.
números reales, se les denomina funciones afines.
Al número 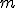 se le llama pendiente de la recta (gráfica de la función), en tanto que a
se le llama pendiente de la recta (gráfica de la función), en tanto que a 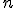 se le denomina ordenada en el origen.
se le denomina ordenada en el origen.
En el siguiente vídeo puedes ver cómo obtener la pendiente y la ordenada en el origen dada la ecuación de la recta:
Vídeo de lasmatematicas.es alojado en Youtube
Caso práctico
Una persona tiene contratada una tarifa para su móvil particular. Le cobran 15 céntimos por el establecimiento de llamada y 6 céntimos por minutos, aunque facturan por segundos, es decir, si hablas medio minuto pagas 3 céntimos.
¿Cuál es la función que da el precio a pagar según el tiempo hablado? ¿Podemos ver una gráfica de esta situación?
Caso práctico
Otra oferta de la compañía telefónica es la tarifa plana de voz por 35 €/mes, incluyendo todas las llamadas a fijos y móviles de cualquier compañía.
¿Cómo sería ahora la función?
Importante
Las funciones que gráficamente se representan mediante una recta son:
- La función afín: y = mx + n, con m y n números reales.
- La función lineal o de proporcionalidad: y = mx, con m un número real, que pasa por el origen de coordenadas.
- La función constante: y = n, con n un número real, que es una recta horizontal.
Por ejemplo:
- y=2x sería una función de proporcionalidad.
- y = 3x - 4 sería una función afín.
- y = 8 sería constante.
Como puedes ver, las funciones lineales y constante, son casos particulares de la función afín.
En la función lineal, n = 0 y en la constante, m = 0.
Las funciones lineales y afines, también se llaman funciones polinómicas de grado 1, pues aparece la variable dependiente "y", igualada a una expresión algebraica con x que es un polinomio de grado 1.
Comprueba lo aprendido
En la siguiente escena puedes practicar con estos conceptos:
Escena de Juan Jesús Cañas Escamilla / José R. Galo Sánchez en Proyecto Descartes. Licencia CC
Comprueba lo aprendido
Por último, veamos cómo representar gráficamente una función afín:
Vídeo de lasmatematicas.es alojado en Youtube
Caso práctico
Representa la gráfica de la función 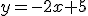 .
.
Ejercicio Resuelto
Representa la gráfica de la función 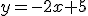 .
.