1.1 Funciones lineales
Ejemplo:
 |
| Fotografía en Flickr de Paco CT bajo CC |
La recta de meta del circuito de Bahrein en Shakir mide algo más de un kilómetro. Un coche de Fórmula 1 realiza un tramo de ella que mide 870 metros, a una velocidad constante de 80 metros por segundo (288 km/h). Nos interesa saber cómo evoluciona la distancia que recorre en los poco más de 10 segundos que tarda en completarlos.
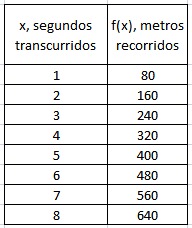
A continuación, expresamos con una tabla y con una gráfica la función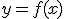 
que relaciona los segundos transcurridos con los metros recorridos por el "Fórmula 1".
 |
 |
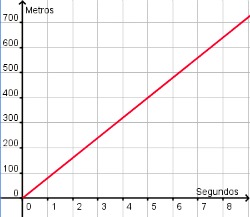Se puede apreciar en la tabla que por cada segundo de variación en la variable independiente existe un aumento de 80 metros en la dependiente y, por tanto, la gráfica de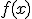 
es una recta que pasa por el origen de coordenadas.
De lo anterior, se deduce que la expresión analítica de la función es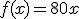 
. Es decir, el tiempo transcurrido y el espacio recorrido son magnitudes directamente proporcionales, ya que las dos variables están relacionadas de manera que cuando una aumenta la otra lo hace también y análogamente cuando disminuye, guardando siempre la misma relación.
A este tipo de funciones, las que tienen por gráfica una recta que pasa por el origen, se les denomina funciones lineales.
Importante
Si dos magnitudes, x e y son directamente proporcionales, la función que las relaciona será de la forma y = m·x. La gráfica es una recta que pasa por el punto (0,0).
A m se le llama pendiente de la recta, y es también la constante de proporcionalidad.
El dominio de una función lineal es todo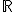 
, el recorrido también es todo 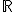, excepto para el caso en que la pendiente 
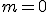. Si la pendiente 
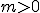, la función lineal es creciente (las gráficas de las funciones siempre se recorren de izquierda a derecha), en tanto que si 
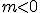, la función es decreciente.
 |
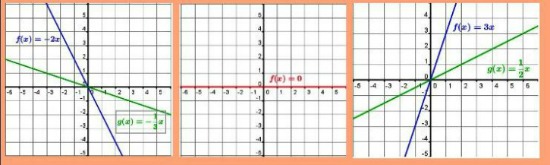| Imagen de elaboración propia. Haz clic para ampliar |
En la imagen superior podemos ver cinco funciones lineales. Dos con pendiente negativa, y por tanto decrecientes; la función lineal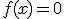 
, también llamada nula; y dos con pendiente positiva, por tanto crecientes. Se puede apreciar que cuanto mayor sea el valor absoluto de la pendiente, más inclinada será la recta.
Veamos otro ejemplo de función de proporcionalidad directa:
Escena de Juan Jesús Cañas Escamilla / José R. Galo Sánchez en Proyecto Descartes. Licencia CC
En la siguiente escena de Geogebra puedes ir cambiando la pendiente y ver cómo se modifica la inclinación de la recta:
Comprueba lo aprendido
Retroalimentación
Verdadero
La variable y es un número por x
Retroalimentación
Falso
La x aparece al cuadrado y además hay sumando un 1.
Retroalimentación
Falso
Es una recta pero no pasa por el origen de coordenadas.Retroalimentación
Verdadero
La gráfica es una recta y pasa por (0,0)