1.2 MAS como proyección de un MCU

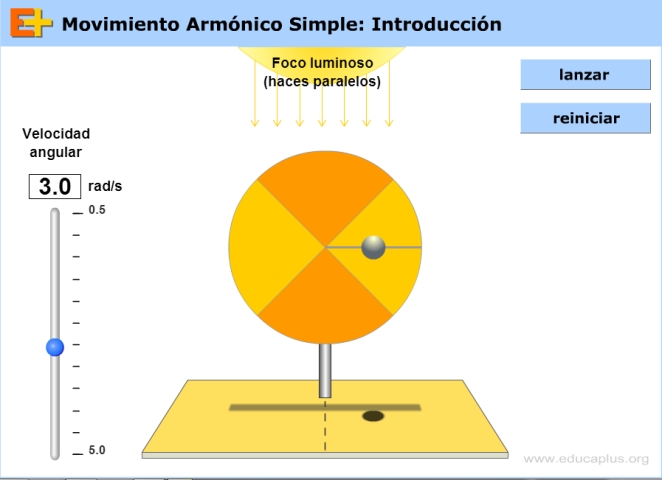
Fíjate en la siguiente animación:

Animación en EDUCAPLUS de Jesús Peñas Cano bajo licencia Copyright con permiso del autor

Quizás hayas observado que hay una bolita que está girando y que es iluminada desde la parte superior, pero tal vez lo más importante es la sombra de ella, que oscila alrededor de un punto de equilibrio con una constancia en algunas magnitudes. Así pues, el movimiento de la sombra corresponde a un movimiento armónico simple.

Se puede constatar que la proyección de un movimiento circular sobre uno de los ejes de coordenadas corresponde a un movimiento armónico simple y a partir de tal situación se puede deducir la ecuación temporal que rige ese movimiento.

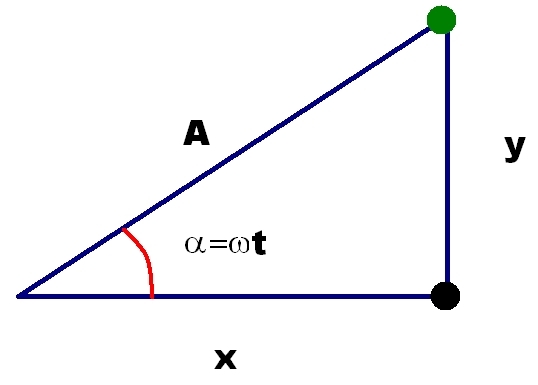
Intentaré aclararte como se obtiene la ecuación que rige el movimiento de la sombra. Para ello, entre la bola, su sombra y el centro establezco un triángulo. Se debe tener en cuenta que el ángulo con respecto al centro va cambiando debido a la velocidad de giro.

Imagen en COMMONS.WIKIMEDIA de FJGAR bajo licencia CC

De la imagen, se puede deducir que la posición de la sombra es, donde cos representa la función coseno:

Como la sombra cambia de posición con el tiempo, se debe colocar el ángulo en función del tiempo. 

Pero si el movimiento no comienza para un ángulo cero, se debe añadir un elemento que se conoce por ángulo de desfase o simplemente desfase.

También, se puede expresar de otra forma y con otra función matemática relacionada con la anterior. Podrás comprenderlo algo mejor si recuerdas algo de trigonometría.

Te aconsejo que visites esta página:El camino más corto: Unos catetos muy listosy vayas al apartado 1.1 "Muy agudo, sí señor". Y hagas lo mismo con la página: El camino más corto: 180º de historia nos contemplan concretamente en el apartado 2 "¿A quién quieres más al seno o al coseno?"