4. Ecuación general de la recta.
Actividad
La forma general de la ecuación de uan recta es una expresión de la forma 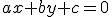
Para calcular la ecuación general de una recta, simplemente utilizamos la forma punto-pendiente o de dos puntos y transformamos la expresión.
Veamos el caso concreto de la ecuación general de la recta que pasa por los puntos 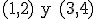 .
.
Usaremos la expresión de la ecuación de la recta que pasa por dos puntos.
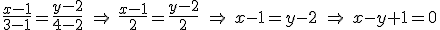
|
De modo análogo podemos calcular la ecuación de la recta en la forma punto-pendiente para calcular la ecuación general.
Estudiemos un caso concreto donde 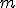 sea
sea 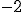 y pase por el punto
y pase por el punto 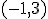 .
.
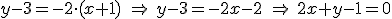
|
En este Applets puedes modificar los puntos A y B para calcular la ecuación general de la recta.
Actividad de rellenar huecos
Calcula la ecuación general de la recta con pendiente 5 y que pasa por 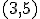 .
.
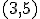 .
.
Actividad de rellenar huecos
Indica la ecuación general de la recta que pasa por 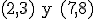 .
.
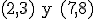 .
.