Resumen

Cuando hablamos de monotonía, nos estamos refiriendo al comportamiento de una función respecto a su crecimiento o decrecimiento.

Sea f una función derivable en un intervalo (a, b), entonces es:

• Creciente en el intervalo (a,b) si 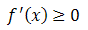en todo el intervalo (a,b)
• Decreciente en el intervalo (a,b) si 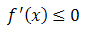en todo el intervalo (a,b)

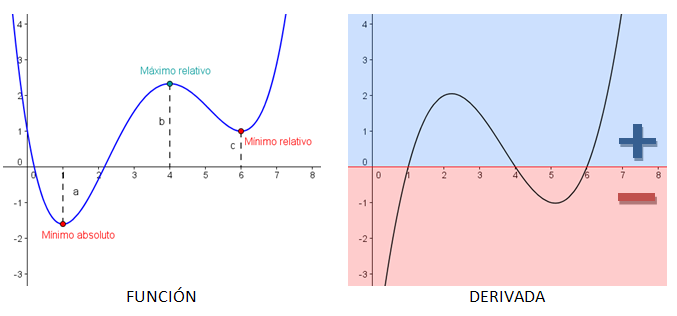
Una función f, continua y derivable en un intervalo (a,b), alcanza sus máximos y mínimos relativos en los puntos del intervalo (a,b) en los que f '(x)=0. Además, si estudiamos la segunda derivada:

• Máximo relativo: f '(x)=0 y f ''(x)<0.
• Mínimo relativo: f '(x)=0 y f ''(x)>0.

En una función dos veces derivable, podemos estudiar la curvatura de la siguiente forma:

• Convexa (U): será convexa en los intervalos donde f ''(x) > 0.
• Cóncava (∩): será cóncava en los intervalos en los que f ''(x) < 0.
• Puntos de inflexión: son los puntos donde cambia la curvatura. Por tanto se cumple que f ''(x)=0.