1. Camino mínimo en la vida cotidiana

El concepto de camino mínimo es fundamental en la teoría de grafos y tiene aplicaciones prácticas extensas. Se refiere a encontrar la ruta más corta o de menor coste entre dos vértices en un grafo, donde el "coste" puede representar distancia, tiempo, o cualquier otra medida que se quiera minimizar.
La aplicación del camino mínimo en los navegadores GPS de vehículos es un claro ejemplo de cómo un concepto matemático puede tener aplicaciones prácticas que afectan de manera positiva a la vida cotidiana de las personas y tiene un impacto profundo en la eficiencia, el ahorro de tiempo y recursos, y la seguridad vial.
Pero el concepto de camino mínimo encuentra aplicaciones en una amplia gama de contextos, algunos de los cuales pueden no ser inmediatamente evidentes.
Aquí se muestran algunos de ellos:
- Planificación de redes eléctricas y de agua: en la ingeniería civil y la planificación urbana, el concepto de camino mínimo se utiliza para diseñar redes de distribución de electricidad y agua. Determinar la ruta más eficiente para extender las líneas eléctricas o tuberías de agua desde fuentes de generación o depósitos hasta los consumidores minimiza los costos de construcción y operación, y reduce la pérdida de energía o agua en el proceso.
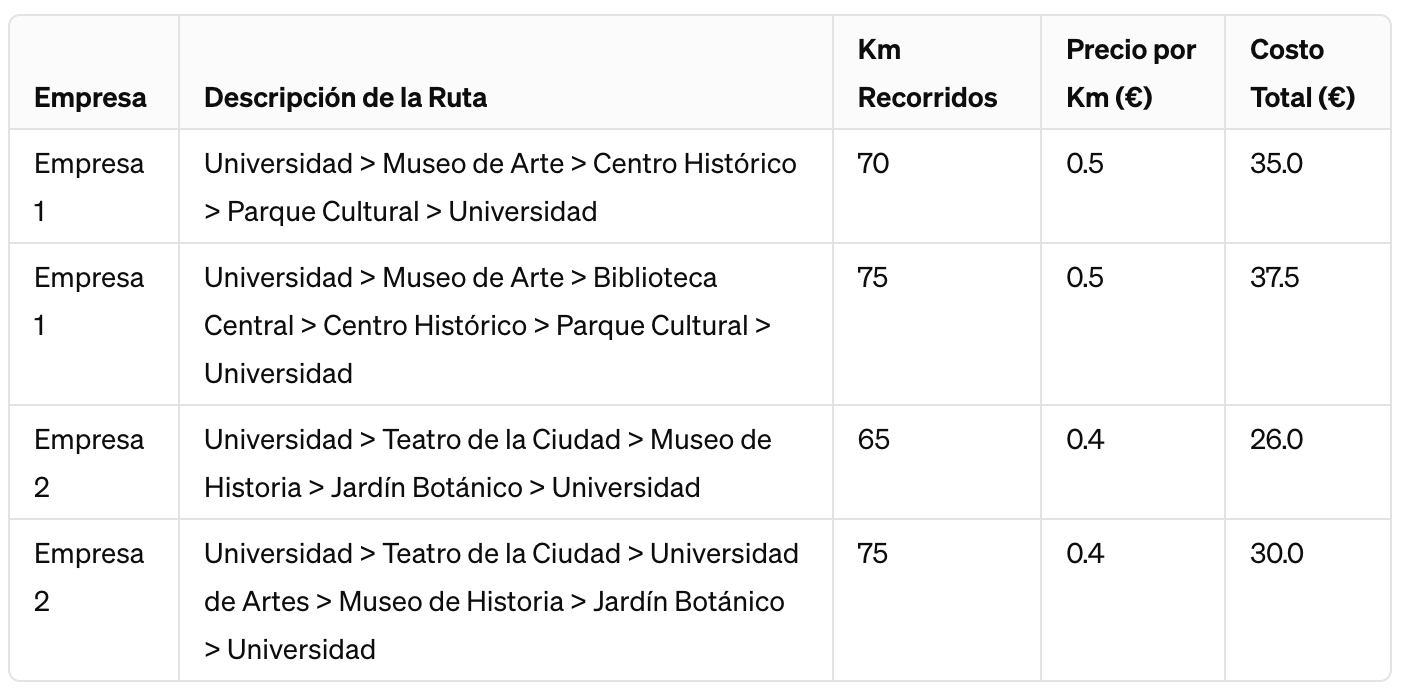
- Optimización de rutas en logística y cadena de suministro: las empresas de logística utilizan algoritmos de camino mínimo para optimizar las rutas de entrega de mercancías. Esto implica calcular el trayecto más corto o más rápido que un vehículo de entrega debe seguir para entregar productos a varios destinos, lo que resulta en ahorros significativos en tiempo y costos de combustible, y en una menor huella de carbono.
- Rutas de evacuación en caso de emergencia: en la gestión de emergencias, especialmente en la planificación de evacuaciones por incendios, inundaciones o terremotos, es crucial determinar las rutas más rápidas y seguras para mover a las personas hacia zonas seguras. Los algoritmos de camino mínimo ayudan a identificar estas rutas, considerando obstáculos, densidad de población y capacidades de las vías de salida.
- Análisis de redes sociales: en el ámbito de las redes sociales digitales, el concepto de camino mínimo se aplica para analizar las conexiones entre usuarios. Por ejemplo, puede utilizarse para encontrar la "distancia" más corta (es decir, la secuencia más pequeña de conexiones) entre dos personas en una red, lo cual es fundamental para funciones como las sugerencias de amistad o la detección de comunidades dentro de la red.
- Diseño de circuitos electrónicos: en la ingeniería electrónica, el diseño de circuitos impresos (PCB) y sistemas integrados se beneficia del uso de caminos mínimos para optimizar la disposición de componentes y conexiones, minimizando el uso de material y mejorando la eficiencia del circuito. Esto es especialmente crítico en dispositivos de alta densidad y alta frecuencia, donde la longitud y disposición de las pistas pueden afectar significativamente al rendimiento.