1. El problema del mapa de los cuatro colores
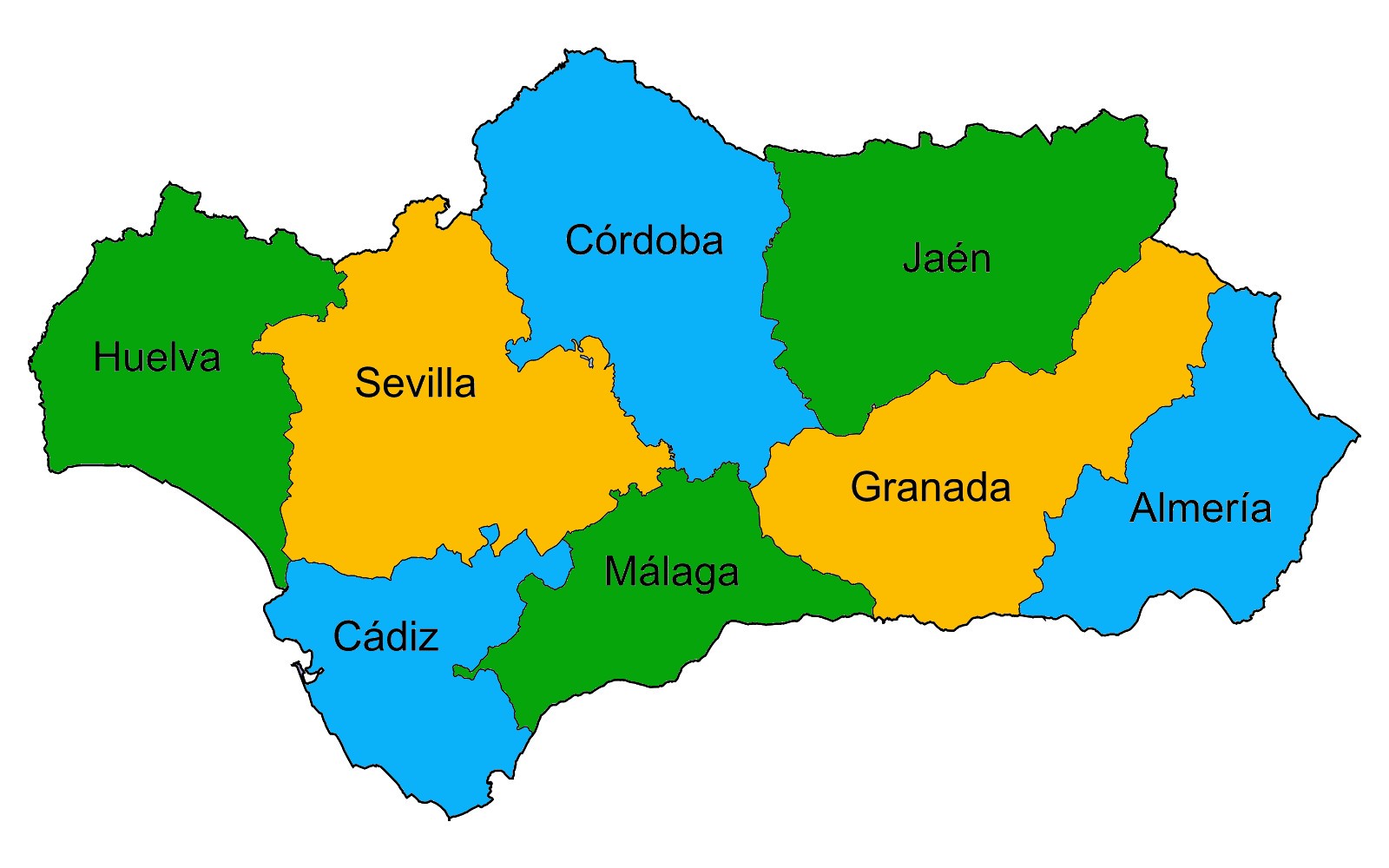
Dado cualquier mapa plano dividido en regiones (como los países en un mapa mundial), ¿es posible colorear las regiones con no más de cuatro colores de tal manera que ninguna región comparta el mismo color con una región adyacente (es decir, aquellas que tienen una frontera común)?
La respuesta a esta pregunta es que sí, sí se puede. La demostración de esta afirmación se conoce como Teorema de los cuatro colores.
El Teorema de los cuatro colores fue propuesto por primera vez en 1852 por Francis Guthrie y fue probado finalmente por Kenneth Appel y Wolfgang Haken en 1976. Su demostración es notable porque fue una de las primeras en las que se utilizó un ordenador para verificar una gran cantidad de casos particulares, lo que generó cierta controversia sobre la naturaleza de la prueba en la comunidad matemática. Sin embargo, la demostración ha sido confirmada y aceptada desde entonces.
El vínculo entre este teorema y la teoría de grafos es fundamental y se establece a través de la representación de mapas como grafos planos. Esta conexión permite aplicar conceptos de la teoría de grafos, en particular la coloración de vértices, para resolver problemas de coloración de mapas.
Pero, ¿cómo se relacionan ambos conceptos? Veamoslo.
Representación de mapas como grafos
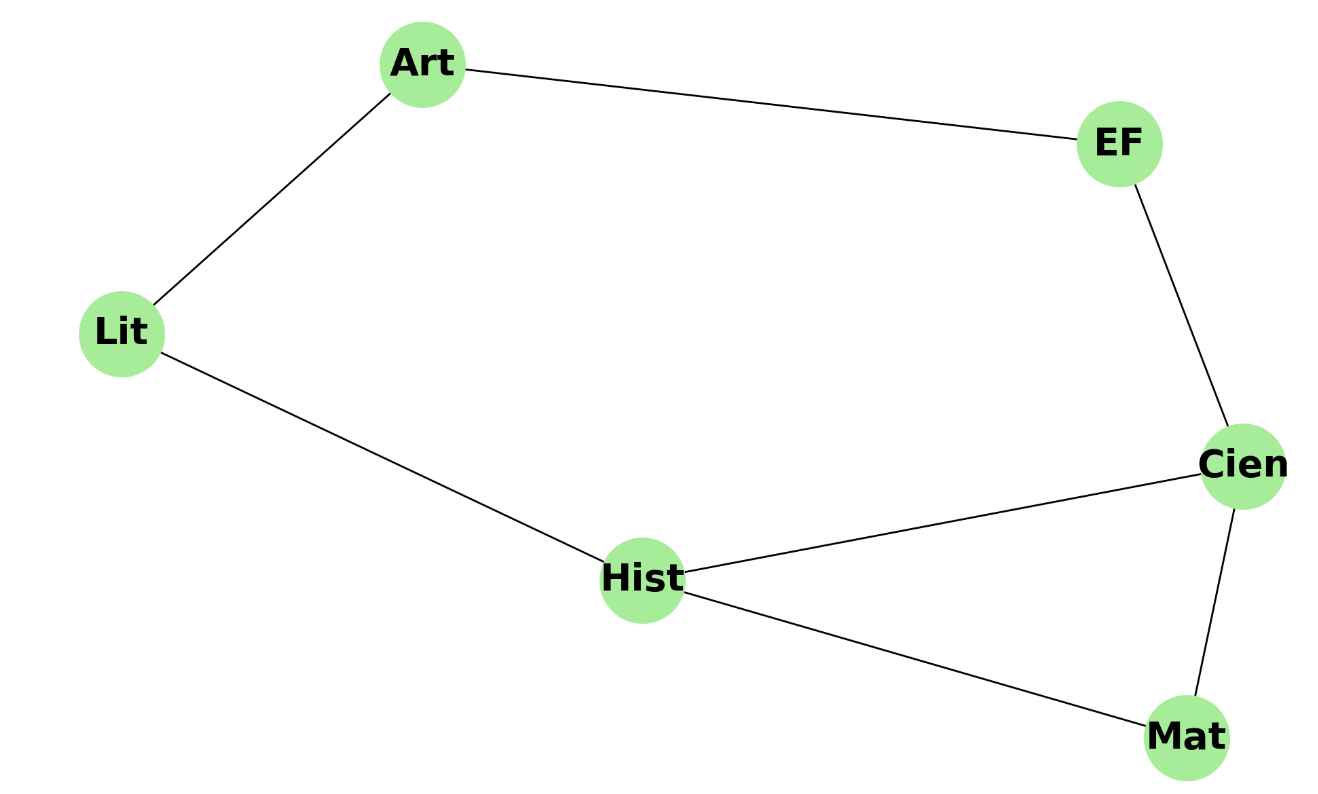
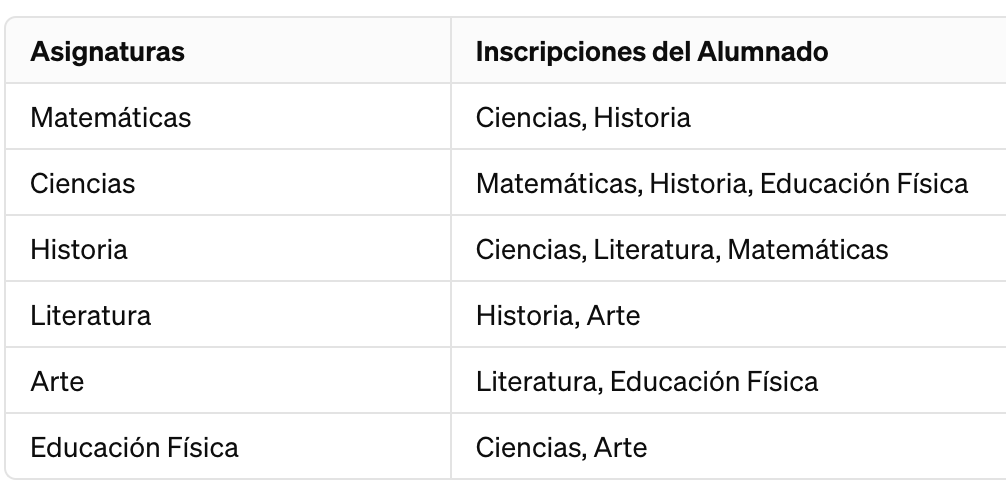
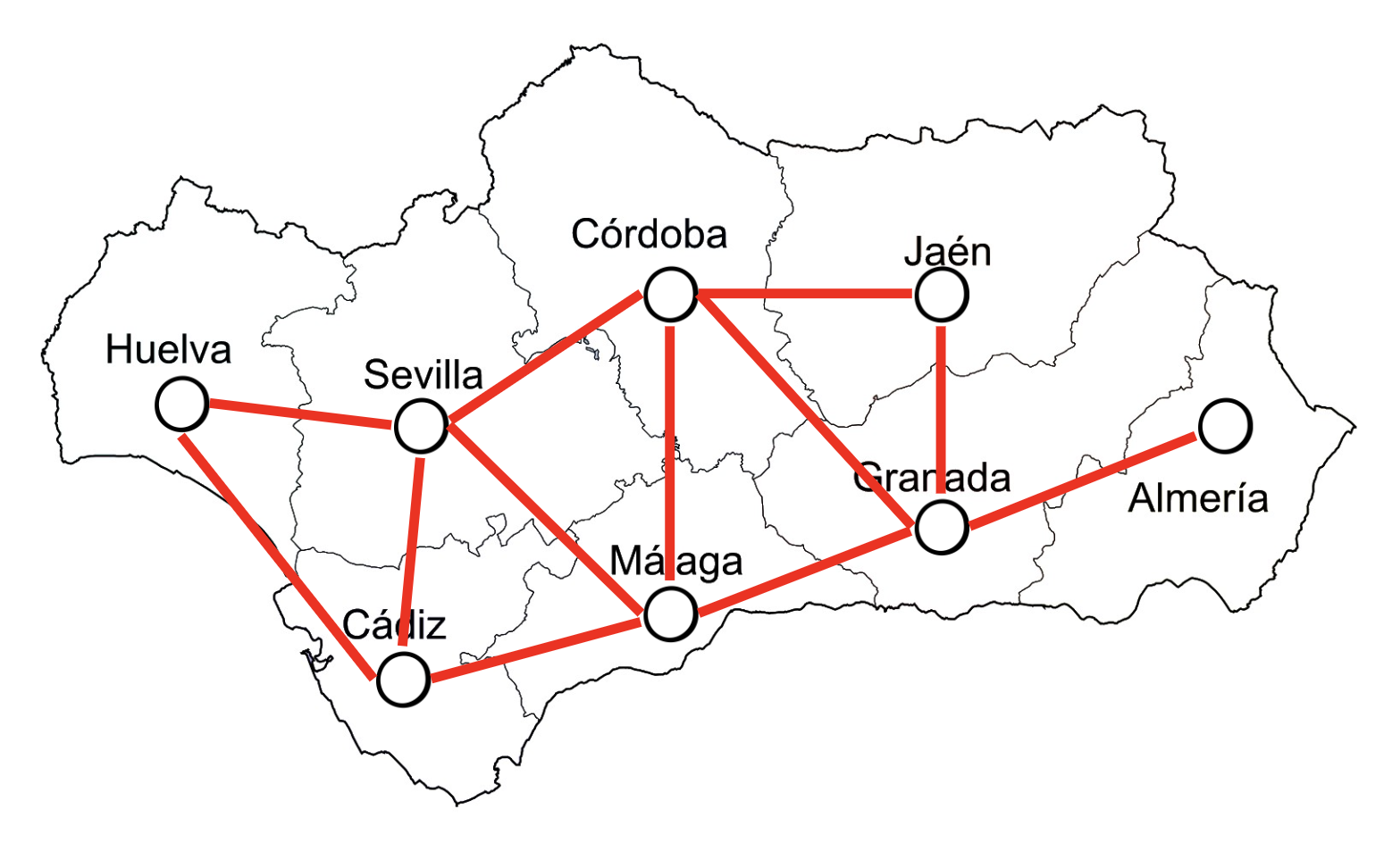
- Vértices del Grafo: cada región del mapa se representa como un vértice en el grafo. Por lo tanto, si un mapa tiene $N$ regiones, el grafo correspondiente tendrá $N$ vértices.
- Aristas del Grafo: dos vértices en el grafo están conectados por una arista si las regiones correspondientes son adyacentes en el mapa, es decir, si comparten una frontera común. Esto significa que el grafo captura la estructura de adyacencia de las regiones en el mapa.
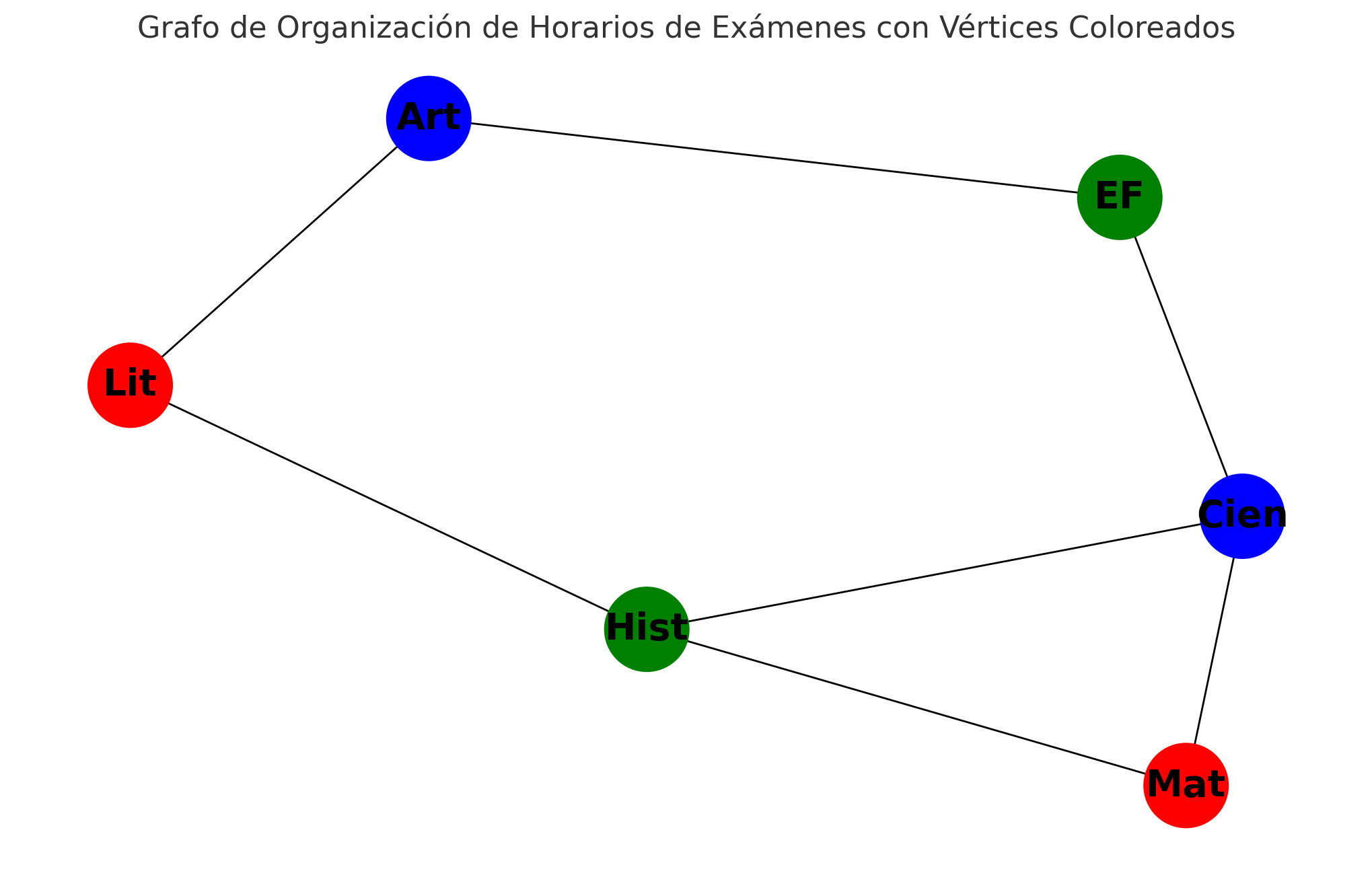
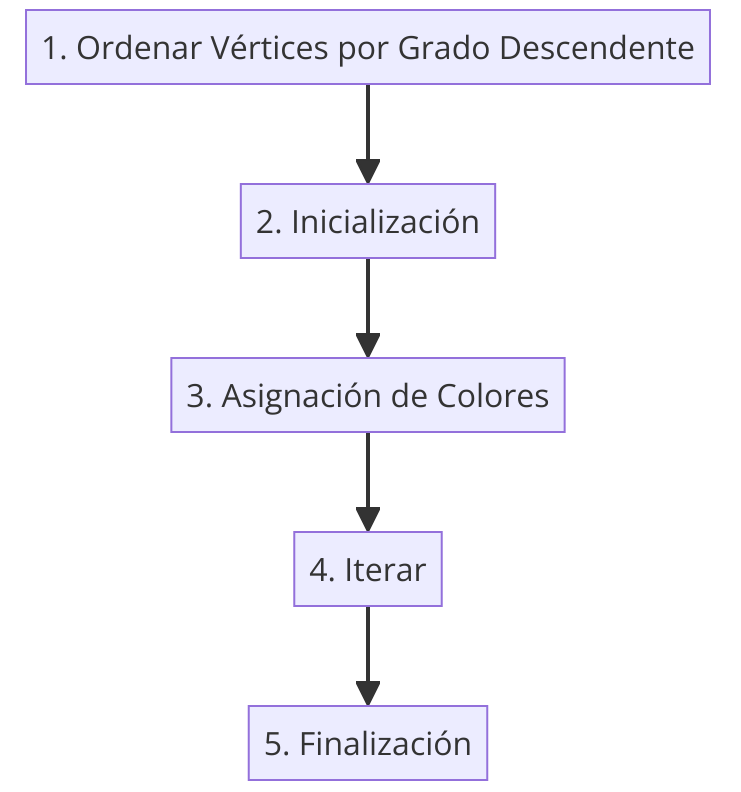
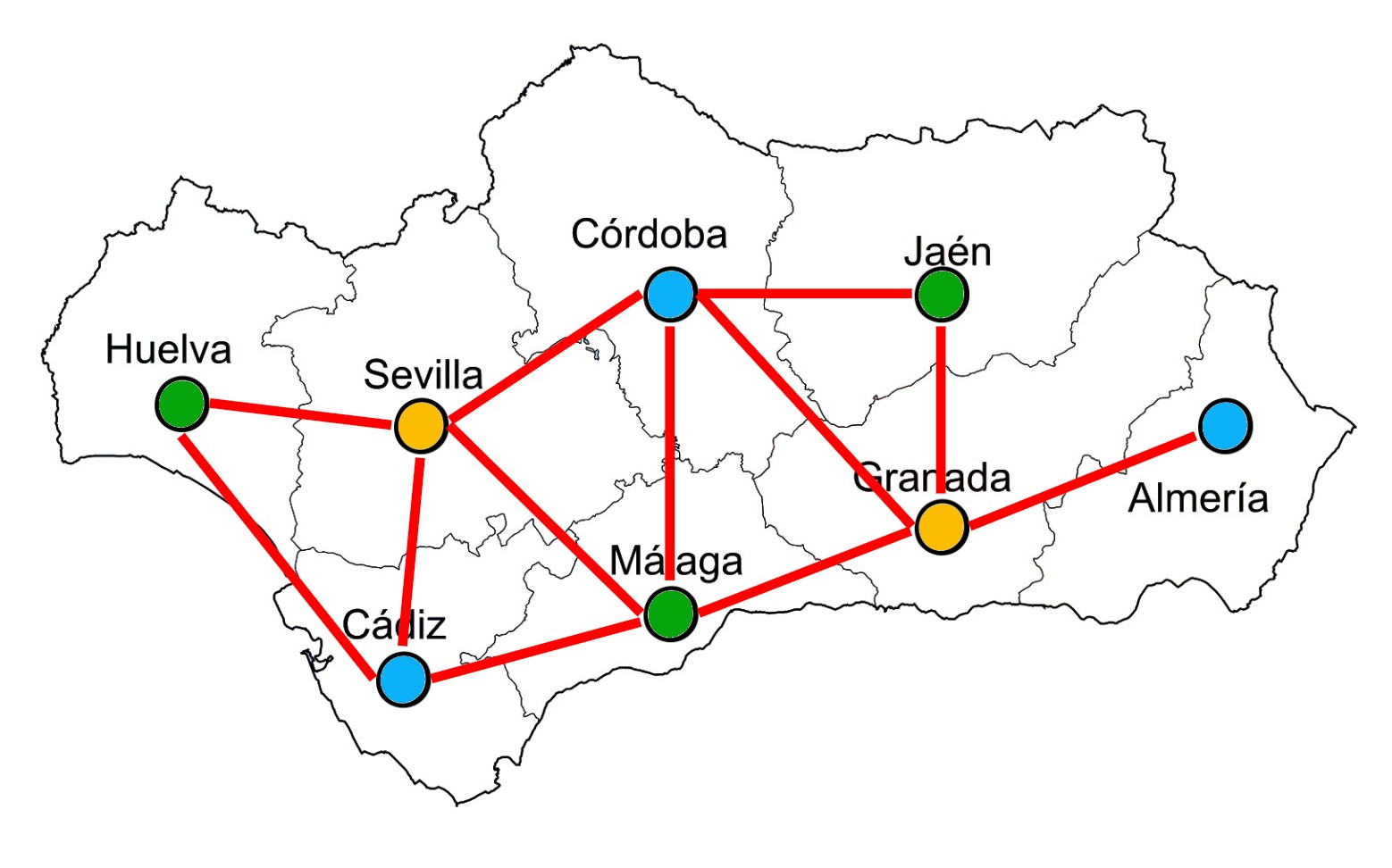
Coloración de Vértices
La tarea de colorear el mapa de manera que ninguna región adyacente comparta el mismo color se traduce en el problema de coloración de vértices en el grafo correspondiente. En este contexto, un "color" es una etiqueta que se asigna a cada vértice (región), y la regla es que vértices conectados (regiones adyacentes) no pueden tener la misma etiqueta (color).