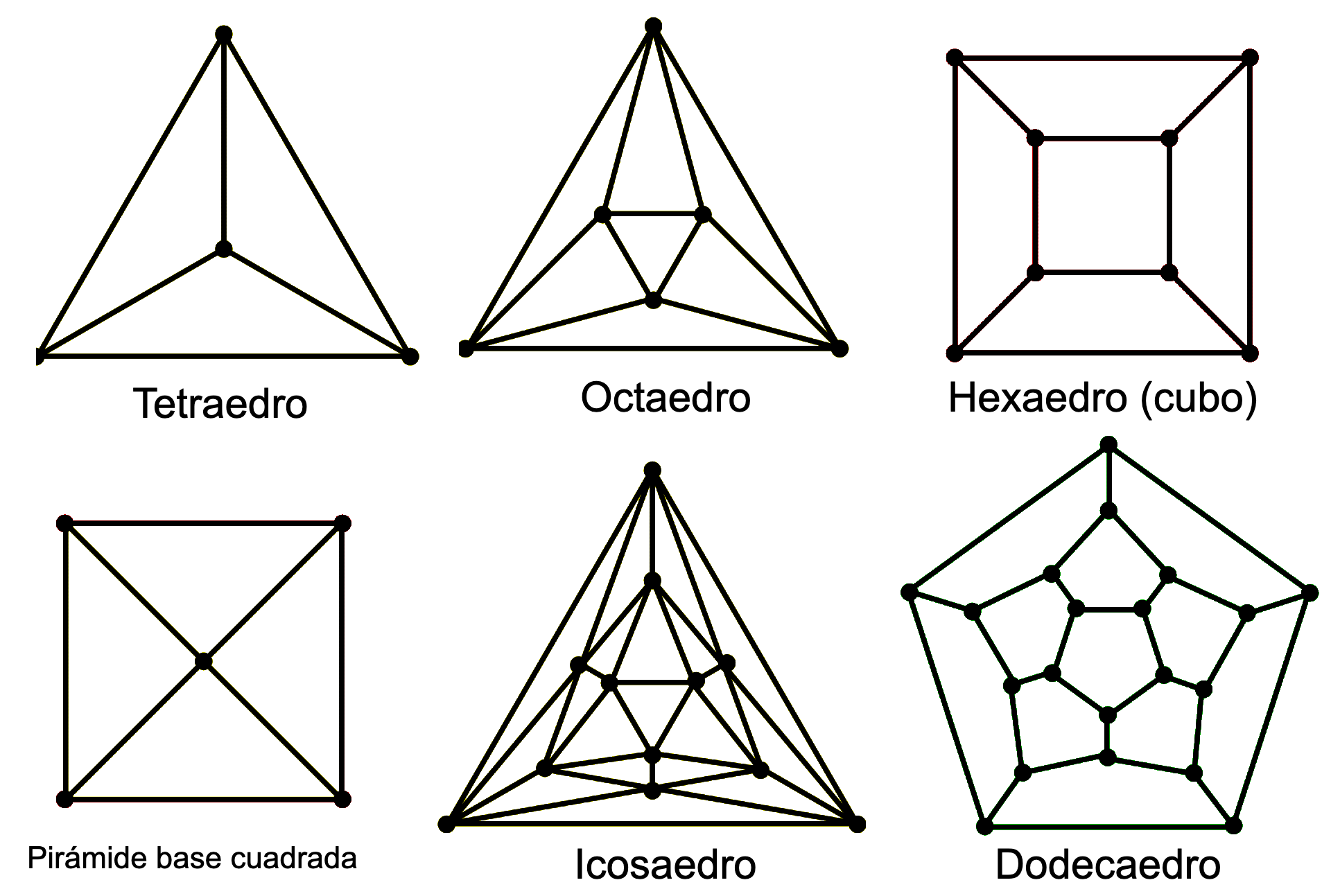Poliedro

Un poliedro es la representación de una región acotada del espacio, la cual está delimitada exclusivamente por polígonos planos.

Los poliedros se clasifican en convexos o cóncavos.

Poliedros convexos. Un poliedro se considera convexo si cumple con la siguiente propiedad: para cualquier par de puntos dentro del poliedro, el segmento de línea que los conecta nunca sale del poliedro.

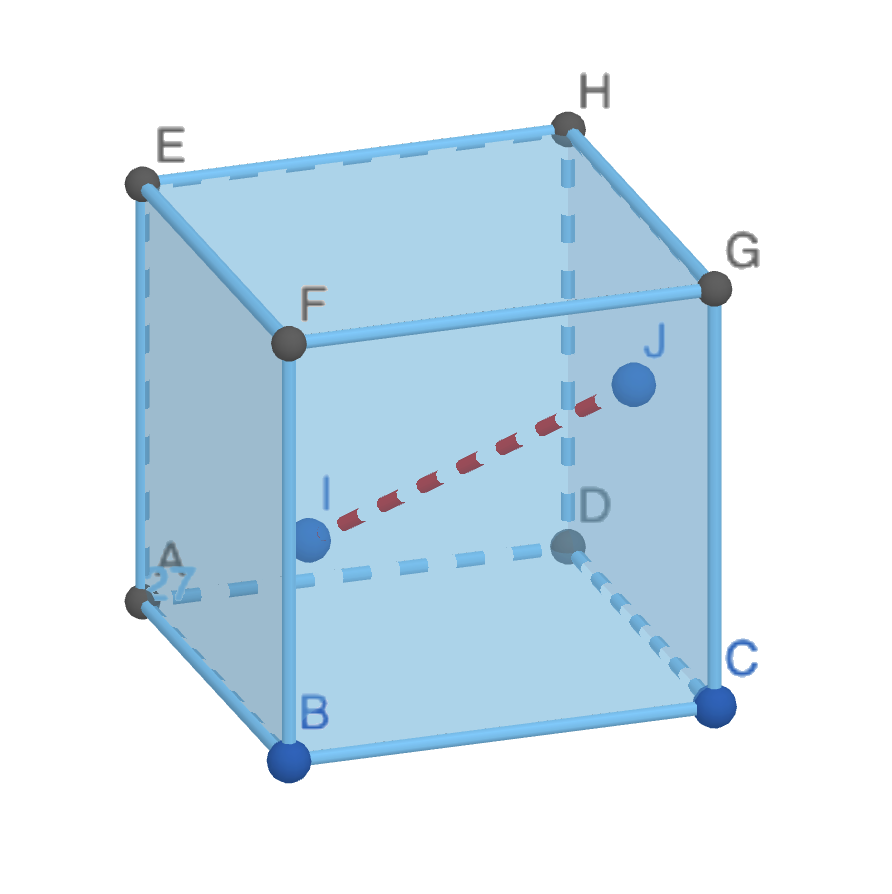
Poliedros cóncavos. Un poliedro se considera cóncavo si existe al menos un par de puntos dentro del poliedro tal que el segmento de línea que los conecta sale del poliedro en algún punto de su trayecto.

Teorema de Euler (para poliedros)

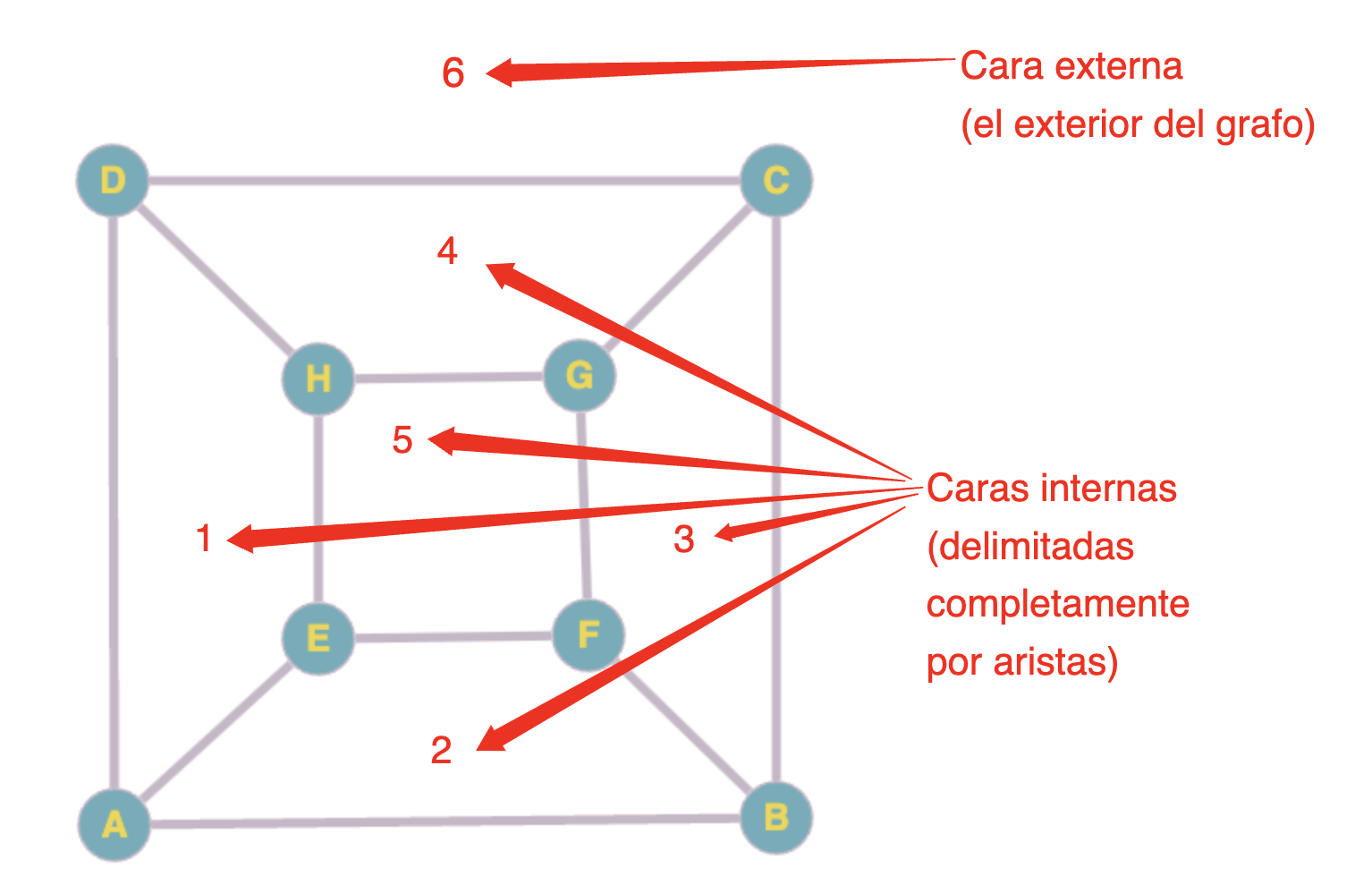
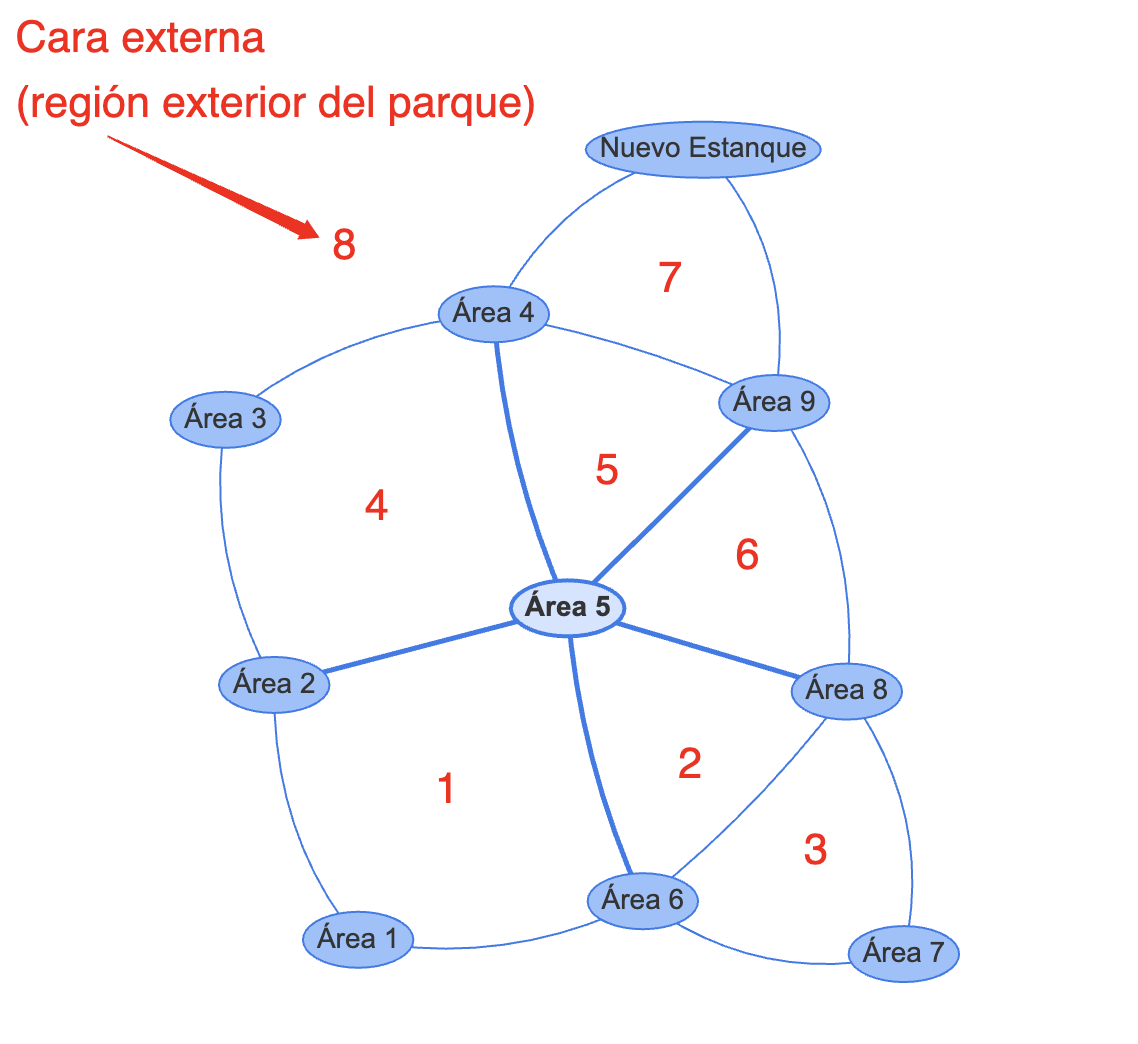
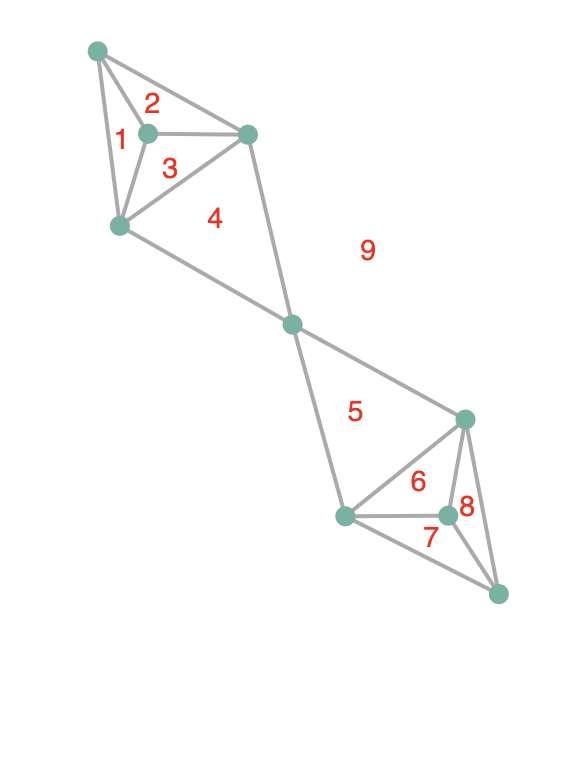
El teorema de Euler para poliedros convexos, también conocido como la fórmula de Euler, es un teorema fundamental en la geometría de los poliedros. Establece una relación entre el número de vértices (V), el número de aristas (A) y el número de caras (C) de un poliedro convexo. La fórmula se expresa como sigue:

$V+C−A=2$

Esta relación es notable porque, sin importar la complejidad del poliedro convexo, siempre se cumple que la suma de los vértices y las caras, menos el número de aristas, es igual a 2. Este teorema es aplicable a cualquier poliedro convexo, incluyendo los sólidos platónicos (tetraedro, cubo, octaedro, dodecaedro, icosaedro) y otros más complejos.

Poliedros Regulares (Sólidos Platónicos)
Los poliedros regulares, también conocidos como sólidos platónicos, son aquellos en los que todas las caras son polígonos regulares congruentes (es decir, todos los lados y ángulos son iguales) y el mismo número de caras se unen en cada vértice. Solo existen cinco sólidos platónicos:

Tetraedro (4 caras triangulares)
Cubo o Hexaedro (6 caras cuadradas)
Octaedro (8 caras triangulares)
Dodecaedro (12 caras pentagonales)
Icosaedro (20 caras triangulares)
Estos poliedros son convexos y se caracterizan por su alta simetría y belleza geométrica.

Grafos poliédricos

Los grafos poliédricos son los que se obtienen a partir de los poliedros mediante un proceso que implica proyectar o mapear las caras, aristas y vértices de un poliedro en una superficie plana sin perder la información esencial del poliedro.

Los poliedros regulares, como los sólidos platónicos, son candidatos ideales para obtener grafos poliédricos debido a su alta simetría y estructura regular, pero cualquier poliedro puede utilizarse.

Para obtener el grafo correspondiente a un poliedro debemos, en primer lugar, identificar todas las caras, aristas y vértices del poliedro. Estos elementos son fundamentales, ya que en el grafo resultante, los vértices representarán los vértices del poliedro, y las aristas del grafo representarán las aristas del poliedro.

Después, el poliedro se "abre" o se proyecta sobre una superficie plana. Así, cada vértice del poliedro se convierte en un vértice del grafo y cada arista del poliedro se convierte en una arista del grafo, conectando los vértices correspondientes.

El grafo obtenido debe ser plano, lo que significa que se puede dibujar en un plano sin que sus aristas se crucen. Todos los grafos derivados de poliedros son planos debido a la naturaleza tridimensional y conexa de los poliedros.

A continuación se muestran los grafos planos correspondientes a los poliedros regulares y a la pirámide de base cuadrada.

Este proceso permite representar la estructura tridimensional de un poliedro en un formato bidimensional, preservando la información sobre cómo los elementos del poliedro están conectados entre sí.

¿Qué son las caras de un grafo?

Las caras de un grafo se refieren a las regiones delimitadas por las aristas de un grafo cuando este se dibuja en un plano sin que sus aristas se crucen, es decir, en el contexto de grafos planos.

Las caras son, por tanto, las áreas cerradas por las aristas de un grafo plano, incluyendo tanto las regiones finitas (interiores) como la región infinita (exterior) que rodea al grafo.

La siguiente imagen muestra el grafo del cubo, identificando tanto las caras internas como la cara externa.

Podemos comprobar que se sigue cumpliendo que  $C+V-A=2$, pues $6+8-12=2$

Teorema de Euler para grafos planos

Teorema de Euler para grafos planos establece que el número de caras, más el de vértices, menos el número de aristas es siempre 2. No debemos olvidar la cara externa en el cómputo total de las caras.

$C+V-A=2$