3.3. Medidas de posición y simetría
Medidas de posición
|
| Imagen en Flickr de tomypelluz bajo CC |
Seguro que muchas veces te habrás encontrado realizando grandes colas: para sacar entradas de un concierto o espectáculo muy requerido, para renovar o entregar alguna documentación, o en situaciones parecidas. En algunos sitios, donde las colas de espera están bien organizadas, nosotros al menos, hemos encontrado de pronto un letrero que indicaba "a partir de aquí 1 hora de espera", unos metros más adelante te encuentras otro de "desde aquí 45 minutos" y así sucesivamente. Es una forma de compartimentar la cantidad de personas que esperan y el tiempo que se tardará en llegar a la entrada o ventanilla. Algo similar hacen los parámetros que vamos a ver en este subapartado.
Se llaman parámetros de posición aquellos que dividen a los datos obtenidos en partes proporcionales, de forma que cada parte tenga el mismo número de elementos. Para poder hacerlo necesitamos que los datos estén ordenados de menor a mayor. A veces se les llama con el nombre genérico de cuantiles. Los hay de tres tipos: cuartiles, deciles y percentiles, aunque vamos a desarrollar el primero y el último.
Importante
-
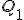: primer cuartil, tiene el 25 % de los datos delante de él y el 75 % detrás.
-
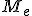: segundo cuartil, que coincide con la mediana. Tiene el 50 % de los datos delante y el otro 50 % detrás de él.
-
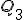: Deja delante de él el 75 % de la distribución y detrás el 25 %.
Para calcular los cuartiles basta generalizar el cálculo de la mediana que ya habíamos visto. Se halla 
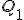y el primer valor cuya frecuencia absoluta acumulada supera ese valor es . Para 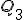debemos hallar 
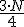y seleccionar aquel valor cuya frecuencia acumulada supera esa cantidad. Hay que recordar, como en la mediana, que si un valor tiene como frecuencia acumulada exactamente ese valor se halla la media aritmética con el valor siguiente.
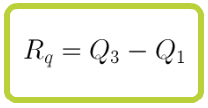
Un estudio conjunto del recorrido y del recorrido intercuartílico nos da información sobre la dispersión de la muestra. Si el recorrido general es grande pero el intercuartílico pequeño, eso indica que hay valores extremos. Si ambos son grandes los datos son dispersos y si ambos son pequeños los datos están muy agrupados respecto a los valores centrales.
Caso de estudio
Para realizar un estudio sobre el gasto farmacéutico en la sanidad pública, nos encargan que hagamos un estudio sobre el número de medicamentos por paciente que se receta en una determinada consulta a lo largo de una semana. Se obtiene la siguiente tabla:
Nº de medicamentos  |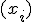
1 | 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Nº de pacientes  |
12 | 24 |
15 |
13 |
9 |
6 |
2 |
1 |
1 |
1 |
Calcula los cuartiles de esa distribución.
Importante
Se definen los percentiles como aquellos parámetros que dividen el conjunto ordenado de valores en 100 partes iguales. De esta manera, el percentil 34, por ejemplo, es aquel que tiene delante el 34% y detrás el 66% restante.
De forma análoga a los cuartiles, para hallar los percentiles dividimos el número total de datos (N) entre 100 y multiplicarlo por el orden del percentil que se busca y después hallar qué valor iguala o sobrepasa a esa cantidad.
Caso de estudio
Como quizás te hayas dado cuenta en el ejercicio anterior, el percentil 50 coincide con la mediana y, de forma análoga,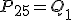 
y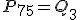 
.
Igual que hay unos parámetros que dividen el conjunto de los valores en 100 partes iguales, existen los deciles que la dividen en 10 partes iguales, pero en lugar de los deciles se suelen utilizar más los percentiles.
Cuando los datos vienen agrupados en intervalos, además de encontrar el intervalo que contiene al percentil correspondiente, es posible precisar el valor del mismo utilizando la fórmula que puedes encontrar en el siguiente enlace:
Medidas de simetría
Existen otras medidas que nos permiten caracterizar la forma de la distribución.
El coeficiente de asimetría de Fisher se define como:
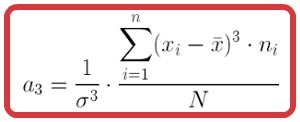
Como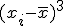 
puede ser positivo o negativo, este coeficiente puede ser positivo o negativo. Atendiendo al signo tenemos los siguientes casos:
 |
|
 |
|
|
|
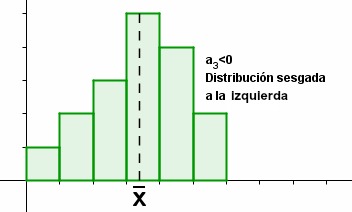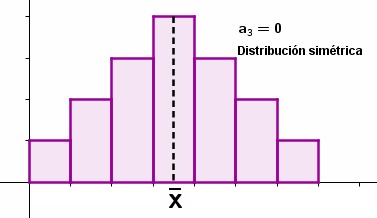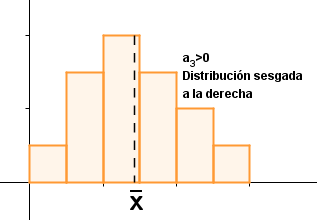
Un coeficiente de asimetría positivo corresponde a distribuciones cuya parte a la derecha de la media es más larga, en un sentido intuitivo, que al otro lado. La asimetría es negativa en el caso opuesto.