3.1. La derivada. Interpretación
Importante
Se define Tasa de variación instantánea en el punto x=a (TVIa) como:


Caso práctico
Calcula la tasa de variación instantánea de la función f(x)=x2 en x=2
Si la TVM era la pendiente de la recta secante (que pasa por los dos puntos (a, f(a)) y (a+h, f(a+h))).
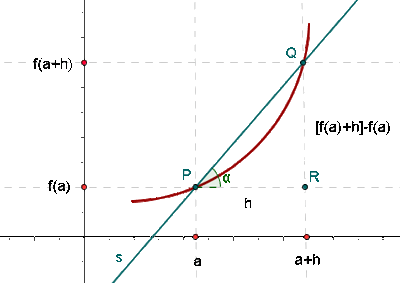
Al hacer que h tienda a 0, los puntos tienden a coincidir. La recta que era secante a la función en los puntos, es ahora tangente a la función en un punto. Para comprobarlo mueve el deslizador "h" en la siguiente escena de Geogebra.
Importante
Si tenemos una función  llamamos derivada de la función en un punto
llamamos derivada de la función en un punto  a la tasa de variación instantánea de la función en el punto
a la tasa de variación instantánea de la función en el punto  y se denota
y se denota  . Así, según la definición tenemos que:
. Así, según la definición tenemos que:

Geométricamente, la derivada de una función en un punto es la pendiente de la recta tangente a la gráfica de la función en dicho punto.
Recuerda que para que exista este límite, por tanto la derivada en dicho punto, deben existir los límites laterales y coincidir.
Así, de la misma forma, podemos definir las derivadas laterales como:
- Derivada por la derecha:

- Derivada por la izquierda:

Caso práctico
 |
Calculemos de forma intuitiva la derivada de la función f(x)=x2 en el punto a=1. Para ello vamos a utilizar la definicion de TVM Construimos la siguientes tablas:
| Intervalo [a,a+h] | [1;1,1] | [1;1,01] | [1;1,001] | [1;1,0001] | [1;1,00001] | ... | [1,1] |
| TVM | 2,1 | 2,01 | 2,001 | 2,0001 | 2,00001 | ... | 2 |
| Intervalo [a,a+h] | [0,99;1] | [0,999;1] | [0,9999;1] | [0,99999;1] | ... | [1,1] |
| TVM | 1,9 | 1,99 | 1,999 | 1,9999 | ... | 2 |
En la primera tabla nos acercamos al punto por la derecha y el resultado es 2.
En la segunda nos acercamos al punto por valores menores (izquierda) y el resultado el 2.
Por tanto, decimos que la derivada de la función f(x) = x2, en x=1 es 2, o escrito de forma más elegante, f '(1) = 2.
Caso práctico
Halla la pendiente de la recta tangente a la gráfica de
en el punto de abscisa x=-2.
Comprueba lo aprendido
Retroalimentación
Verdadero
De la Tasa de Variación Media entre dos puntos.Retroalimentación
Falso
Los sábados , domingos y días de fiesta que no hay actividad, no hay función.Retroalimentación
Falso
Hacer desaparecer el tiempo.... no es posible aún.Retroalimentación
Verdadero
¡Ya se que no viene en el tema pero es una buena forma de terminar! Además tenías un 0,5 de posibilidad.Para saber más
En el siguiente vídeo de la serie Universo Mecánico puedes ver los aspectos históricos que llevaron a la creación de la derivada y algunas de sus aplicaciones en la vida cotidiana. Aparecen también las reglas sobre como calcular derivadas de distintas funciones, algo que veremos en el próximo tema.