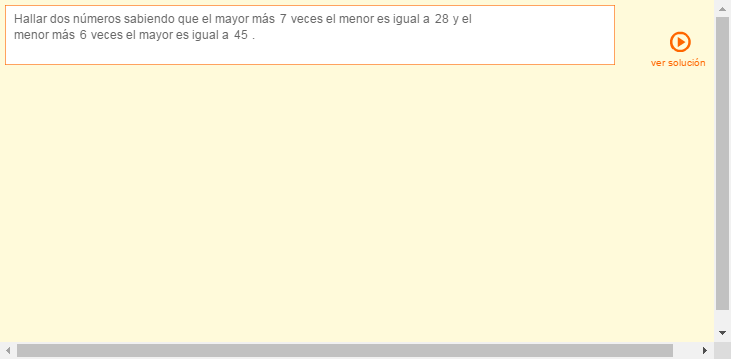
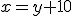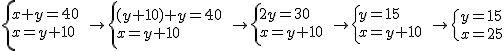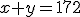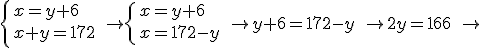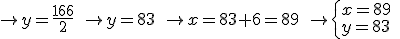3.2. Sistemas lineales de dos ecuaciones con dos incógnitas
 |
| Fotografía en Flickr por Ignacio Conejo bajo CC |
En las dos situaciones mostradas en el punto anterior no hemos podido más que establecer una relación entre las dos incógnitas y dar posibles combinaciones de resultados.
Pero, ni hemos podido determinar un número único de goles marcados por cada uno de los delanteros del F.C Barcelona, ni el número preciso de goles marcados por cada uno de los equipos.
En ambas situaciones nos falta una pista: otra ecuación. Al tener dos incógnitas, para poder encontrar unos valores únicos para los goles marcados, necesitamos al menos dos pistas, es decir, dos ecuaciones.
Si las dos pistas son "buenas", entonces sí que podremos encontrar unos valores únicos para las incógnitas planteadas.
Con las dos pistas tendremos lo que en Matemáticas se conoce con el nombre de sistema de ecuaciones.
Actividad
Un
sistema de dos ecuaciones lineales con dos
incógnitas, como su propio nombre indica, está compuesto por dos ecuaciones de primer grado.
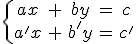
Resolver
el sistema
es encontrar una solución común de ambas ecuaciones. Por tanto, una
solución del sistema es una pareja de valores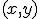 
que cumple ambas ecuaciones de manera simultánea.
Resolución de sistemas de ecuaciones: Método gráfico.
Vamos a ver distintas maneras de resolver un sistema de ecuaciones lineales. Comenzaremos con el método gráfico que nos mostrará que resolver un sistema de ecuaciones no es otra cosa que calcular los puntos de corte de sus dos rectas asociadas.
Actividad
Si interpretamos esto desde un punto de vista gráfico, una solución del sistema vendrá dada por las coordenadas 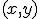de un punto que pertenezca a las dos rectas, esto es, de un punto de corte de las dos rectas.
Por tanto, para resolver un sistema de ecuaciones, por el método gráfico, debemos:
- Representar gráficamente la recta de cada una de las ecuaciones.
- Determinar los puntos comunes de ambas rectas.
En el siguiente applet aparecen multitud de ejemplos de sistemas resueltos para que puedas practicar de manera autónoma. Pulsa sobre el botón gris situado debajo del sistema para ver "OTRO EJEMPLO".
Como puedes ver, dibujar las rectas de cada una de las ecuaciones no es una tarea excesivamente compleja. Basta despejar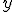 
en función de 
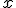, elaborar una pequeña tabla de valores y representar los puntos obtenidos.
AV - Pregunta de Elección Múltiple
Actividad
Un sistema es compatible si tiene solución e incompatible si no la tiene.
Un sistema es determinado si tiene un número finito de soluciones e indeterminado si tiene infinitas soluciones.
Resolución de sistemas de ecuaciones: Métodos analíticos
Como hemos visto en el apartado anterior, un sistema se puede resolver gráficamente. Pero en muchas ocasiones, este método presenta algunos inconvenientes.
En el caso de que no dispongamos de una herramienta informática preparada para representar las gráficas, estaremos obligados a construir una tabla con los puntos, para posteriormente realizar la representación de las rectas a mano.
También nos puede ocurrir que, una vez representadas las rectas, el punto de corte esté muy alejado del origen de coordenadas o que no tenga las coordenadas enteras. Situaciones estas, que suelen significar un obstáculo para encontrar la solución exacta.
Todos los inconvenientes señalados anteriormente justifican de manera clara la necesidad de que existan métodos de resolución de sistemas analíticos, es decir, realizando operaciones.
Veamos los tres métodos más clásicos, que consisten en buscar sistemas equivalentes, que son aquellos que tienen la misma solución, cada vez más sencillos:
 |
| Imagen de elaboración propia |
Como en apartados anteriores, antes de que te pongas manos a la obra, te ofrecemos una lista de reproducción de juanmemol sobre resolución de sistemas lineales de dos ecuaciones con dos incógnitas. En ella puedes encontrar 21 vídeos, en los que aparecen ejercicios clásicos, problemas e incluso una actividad de la prueba de acceso para mayores de 25 años planteada en Cataluña en el 2010.
AV - Actividad de Espacios en Blanco
A las dos situaciones relacionadas con el fútbol que vimos en el punto anterior, le vamos a añadir una nueva pista.
Plantea en cada uno de los casos un sistema de dos ecuaciones con dos incógnitas, resuélvelos por el método que prefieras y completa los espacios en blanco que nos dan la solución.
Ejemplo o ejercicio resuelto
A un partido benéfico celebrado en el estadio Ramón Sánchez Pizjuan, de Sevilla, han asistido 42.000 espectadores. Se ha puesto a la venta únicamente dos tipos de entradas, a un precio de 15 € para los adultos y entradas infantiles a 6 €. La recaudación total ha sido de 612.000 €. ¿Cúantas entradas de cada tipo se han vendido?
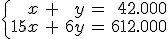multiplicamos los dos miembros de la primera ecuación por -15, tendremos que el coeficiente de x en ambas ecuaciones es opuesto, -15 y 15.
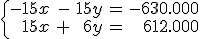
Si ahora sumamos las dos ecuaciones miembro a miembro, haremos desaparecer la
, y nos quedará una ecuación con una única incógnita, . Si la resolvemos tendremos el valor numérico de .
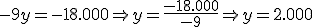
Posteriormente, sustituiremos este valor de 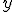en la primera ecuación, calculando el valor de .
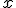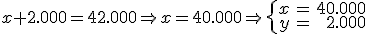
Hemos encontrado la solución de una manera rápida, simplemente consiguiendo coficientes opuestos en una de las incógnitas. Lo que hemos es aplicar el método de reducción.
AV - Reflexión
Uno de los motores que propulsa el lanzamiento del cohete Ariane 5 es el Vulcain 2.
Durante los 540 segundos que dura su funcionamiento consume las 155 toneladas de combustible que contiene, compuestas exclusivamente de oxígeno e hidrógeno líquido.
Por cada tonelada de hidrógeno el Vulcain carga 5,2 toneladas de oxígeno.
Plantea y resuelve un sistema de dos ecuaciones con dos incógnitas que nos permita saber la cantidad exacta de oxígeno e hidrógeno líquido que almacena en el motor.
Caso de estudio
 |
Curso 2009/2010
Determine los coeficientes de la ecuación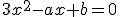 
para que sus soluciones sean los valores 3 y -2.