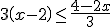2.2. Inecuaciones lineales

Desigualdades e inecuaciones

Observa la siguiente imagen y procura relacionarla con el nombre del epígrafe de este apartado, desigualdades e inecuaciones.

Noticias con inecuaciones
Imagen de elaboración propia con recortes de titulares de elpais.com del día 14/05/2012

Probablemente lo primero que se os venga a la cabeza es una desigualdad del tipo social, puede que incluso te hagas preguntas como: ¿es justo que una persona haya ocupado un puesto de relevancia basándose en una mentira? o ¿nos merecemos que suba el tipo de interés por las dudas de los bancos?, incluso ¿era necesaria la ocupación del territorio afgano? Es una lástima que no podamos entrar en estos detalles, porque las desigualdades con las que nos disponemos a trabajar son otras, y si no fíjate en las frases que están recuadradas y en la siguiente actividad.

 

AV - Pregunta Verdadero-Falso

En el día de ayer, las temperaturas medias en cinco capitales europeas fueron:
Capital Madrid Londres
Berlín
Moscú
Roma
Temperatura (ºC)
 16 8 -1 -5 8
Indica la veracidad o falsedad de la siguientes afirmaciones:

Pregunta 1

En Madrid hace más calor que en Londres.

Pregunta 2

En Berlín hace más frío que en Moscú.

Pregunta 3

En Londres hace la misma temperatura que en Roma.

Actividad

Recordamos que, dados dos números y 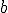pueden darse únicamente tres relaciones entre ellos:

  • es menor que 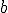 y lo expresamos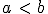

  • es igual a 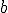 y lo expresamos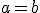

  • es mayor que 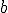 y lo expresamos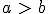

La segunda relación se denomina igualdad y cuando aparecen letras además de cifras numéricas, dan origen a las ecuaciones.

Las relaciones primera y tercera se denominan desigualdades y cuando aparecen letras además de cifras numéricas, dan origen a las inecuaciones. Con ellas trabajaremos a continuación.

AV - Actividad de Espacios en Blanco

Ordena la lista de temperaturas de la tabla anterior, en orden ascendente (y luego en orden descendente), colocando entre cada dos valores el signo <, =, >, que corresponda.

En orden ascendente (de menor a mayor): < 8

En orden descendente (de mayor a menor): 16 >

Habilitar JavaScript

AV - Pregunta Verdadero-Falso

¿Te has parado a pensar cómo se comportan las desigualdades numéricas cuando se someten a variaciones (aumento, disminución, ...)? Enseguida lo vas a descubrir.

Pregunta 1

  1. ¿Qué ocurre si aumenta la temperatura 2 ºC en Moscú y en Roma? ¿Sigue haciendo más frío en Moscú que en Roma?

Pregunta 2

  1. Si disminuye 2 ºC la temperatura en ambas ciudades, podemos afirmar ahora que hace más frío en Roma que en Moscú.

Pregunta 3

  1. Si se triplica la temperatura en ambas ciudades, hará más calor en Moscú que en Roma.

Pregunta 4

  1. En las noticias, dan el siguiente titular:
"Hoy 15 de Diciembre, se aprecian los efectos del cambio climático en las temperaturas de ciertas capitales europeas. Se ha invertido la situación, Moscú presenta una temperatura atípica para estas fechas con 10 ºC. Al mismo tiempo una ola de frío se encuentra situada sobre Roma donde se han alcanzado temperaturas de -16 ºC."
Por tanto, podemos afirmar que ahora sí que hace más calor en Moscú que en Roma.

Cada una de las situaciones de la autoevaluación anterior muestra el comportamiento de una desigualdad numérica cuando se suman, restan, multiplican o dividen los dos miembros de una desigualdad por una misma cantidad.

A continuación, se presenta de manera resumida cada uno de los casos.

Actividad

  • Si a los dos miembros de una desigualdad se le suman o restan un número positivo, la desigualdad no cambia de sentido.

  • Si a los dos miembros de una desigualdad se le suman o restan un número negativo, la desigualdad no cambia de sentido.

  • Si se multiplican o dividen por un número positivo los dos miembros de una desigualdad, entonces la desigualdad no cambia de sentido.

  • Si se multiplican o dividen por un número negativo los dos miembros de una desigualdad, entonces se invierte y cambia de sentido.
velocidad
Foto de Flickr por PixelPlacebo bajo CC

Inecuaciones

Si eres un buen conductor seguro que sabes que en las autopistas españolas debemos circular a una velocidad inferior o igual a 120 km/h.

Si llamamos a la velocidad en kilómetros por hora a la que conducimos, la expresión algebraica que representa esa situación vendría dada por: .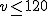

Si circulamos a velocidad superior a 120 km/h estaremos poniendo en peligro nuestra seguridad y seremos sancionados. En este caso la expresión algebraica sería: .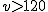

Las dos expresiones anteriores se denominan inecuaciones o desigualdades.
Lo primero que llama la atención de las inecuaciones es que tienen infinitas soluciones. Esa es una característica esencial de las inecuaciones.
Trabajaremos exclusivamente con inecuaciones de una incógnita.

Actividad

Una inecuación es una expresión matemática con cifras y letras caracterizada por tener alguno de los signos de desigualdad 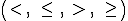, mostrando un desequilibrio entre cifras y letras.

Una inecuación respeta todas las propiedades vistas para las desigualdades numéricas, que son:

  • No cambia de sentido, si se suman o restan números a ambos miembros, ya sean positivos o negativos.

  • Tampoco cambia de sentido, si se multiplican o dividen ambos miembros por un número positivo.

  • Cambia de sentido, se desequilibra hacia el otro lado, si se multiplican o dividen ambos miembros por un número negativo.

Actividad

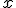Resolver una inecuación es encontrar el conjunto de números reales que cumplen la desigualdad. Este conjunto infinito de soluciones será un intervalo de la recta real.

El proceso de resolución consiste en realizar transformaciones (suma, resta, multiplicación o división) de una misma cantidad a ambos miembros de una inecuación, hasta llegar a una inecuación en la que la incógnita esté sola en uno de sus miembros, en el otro haya un número y, entre ambos, uno de los signos de desigualdad.

El objetivo de estas transformaciones es llegar a obtener uno de los siguientes modelos (donde es la incógnita y un número real)




Finalmente, la solución de la inecuación vendrá dada por los infinitos valores que verifican esta última desigualdad. Es decir, todos los puntos del intervalo que tienen por extremo inicial (o final) al valor .

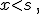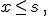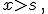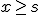AV - Pregunta de Selección Múltiple

Pregunta

  1. Tenemos la siguiente inecuación: . 

    2. ¿Cuáles de los siguientes valores son solución de esa inecuación?

Respuestas







Retroalimentación

Pregunta

  1. ¿Cuáles de las siguientes inecuaciones, tienen como solución la siguiente representación gráfica?

 

Solución

Respuestas







Retroalimentación

Como en algunos apartados anteriores, te ofrecemos unos vídeos del profesor juanmemol. En este caso es una lista de reproducción que consta de 18 vídeos de inecuaciones de primer grado y aquí te mostramos un ejemplo:

 

Ejemplo o ejercicio resuelto

Resuelve la siguiente inecuación y representa la solución obtenida:


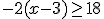
AV - Pregunta de Elección Múltiple

Pregunta

¿Cuál es el conjunto de soluciones de la siguiente inecuación?

 

Respuestas







Retroalimentación

Caso de estudio

 

 logotipo

Curso 2010/2011

Halle el conjunto de soluciones de la inecuación: