1.1. Expresiones algebraicas
Símbolos y números
En algunos aspectos de nuestra vida diaria utilizamos símbolos para referirnos a determinadas objetos, mensajes o situaciones. No tienes más que pensar en el reciente "lenguaje sms" creado para chatear o enviar mensajes de texto.
 |
| Fotografía en Flickr por katielips bajo CC |
El lenguaje algebraico es algo menos moderno pero sin duda bastante más útil ya que nos permite:
- Percibir las estructuras lingüísticas subyacentes y su relación con las operaciones matemáticas, independientemente de la clase de números que aparezcan en ellas.
- Representar, generalizar y formalizar patrones y regularidades.
- Crear modelos para problemas procedentes de la propia matemática (aritméticos, geométricos...) o de la vida cotidiana, financieros, físicos, etc. La modelización algebraica de los problemas desarrolla capacidades de representación, análisis verbal, búsqueda de relaciones y funciones, solución mecánica, análisis de soluciones, alcance de estas y generalización de los procesos.
- Reducir los tipos de problemas y unificar las técnicas de solución, destacando la importancia de herramientas y técnicas como el uso de funciones y operaciones.
Ejemplo o ejercicio resuelto
Ana colabora en una asociación como voluntaria. Dependiendo del tiempo del que disponga, puede desarrollar su labor en Jornada Completa (8 horas), a Media Jornada (4 horas) o a Horas Sueltas.
Cada día, cuando los voluntarios llegan a la sede de la asociación, anotan el tipo de jornada que van a dedicar en una ficha como esta:
| Nombre |
Jornada Completa |
Media Jornada |
Horas sueltas |
||||||||||||
| Ana |
x | x |
x |
x |
x |
x | x | ||||||||
Y al final del mes, la asociación genera un resumen de la dedicación de sus voluntarios:
| Nombre |
C | M | S |
| Ana |
4 |
2 |
1 |
| Manuel |
6 |
0 |
2 |
| Javi |
1 | 7 |
6 |
| Marta |
12 |
1 |
0 |
Como ves, C, M y S son letras que equivalen a diferentes números según cada caso. En Matemáticas, a estas letras las llamaremos variables. Las variables no solo nos sirven para organizar información, sino también para trabajar con números de una forma generalizada. Es decir, no necesito saber cuánto vale C para poder hacer determinados cálculos.
Por ejemplo, si a final de mes quiero saber cuántas horas ha dedicado alguien en días a jornada completa, tendré que multiplicar el número de días que ha tenido esa jornada (C) por 8, que es el número de horas que se dedican esos días. Es decir: C·8
Cuando trabajamos con números y letras, hay algunas reglas que debemos seguir. Una de ellas es que, si multiplicamos un número por una letra, primero escribiremos el número y luego la variable. En nuestro caso quedaría: 8·C
Otra regla es que, si estamos multiplicando un número por una variable, no es necesario escribir el símbolo del producto. Por lo tanto, el número de horas que dedica alguien mensualmente en Jornadas Completas será 8C
Sabiendo esto ¿serías capaz de escribir con números y las variables C, M y S cuántas horas dedica un voluntario mensualmente?
Si pinchas en la siguiente imagen descubrirás multitud de símbolos matemáticos, algunos ya conocidos y muchos otros por conocer. Con casi toda seguridad que en alguna ocasión (no muy lejana) tendrás que recurrir a esta fuente:
 |
| Imagen de www.3con14.com bajo CC |
 |
| Fotografía en Flickr por brainware3000 bajo CC |
Como ya hemos visto el lenguaje algebraico está formado por números, símbolos matemáticos y letras.
Cuando pasamos del lenguaje ordinario al lenguaje algebraico ponemos de manifiesto los datos (que simbolizamos por letras), las operaciones que los ligan (a través de símbolos preestablecidos) y las relaciones entre los mismos (por ejemplo, la de igualdad).
Es costumbre en ciertos campos de las ciencias usar letras determinadas según el objeto con el que se esté trabajando. Así por ejemplo, si manejamos números naturales en sucesiones, es usual utilizar las letras m y n, para simbolizar dichos números. Los números pares se simbolizan con 2n y los impares con 2n+1.
Otro ejemplo, en geometría se suelen utilizar letras mayúsculas para referirnos a los ángulos, puntos, superficies, volúmenes... mientras que se utilizan letras minúsculas para las medidas lineales.
En Física, en el estudio del movimiento el espacio se simboliza por e, la velocidad por v y el tiempo por t.
Aunque en teoría se podría utilizar cualquier letra para simbolizar las magnitudes anteriores, respetar el lenguaje preestablecido es síntoma de conocimiento y soltura.
Expresiones algebraicas
En la siguiente presentación vamos a descubrir cómo pasar del lenguaje ordinario al lenguaje algebraico y el resultado de este cambio: las expresiones algebraicas.
Actividad
Cada expresión algebraica tiene un significado. De hecho, cuando tenemos un problema, intentamos traducirlo al lenguaje algebraico mediante una expresión. Mira los siguientes ejemplos
|
Enunciado
(lenguaje usual) |
A un número le sumamos 4 unidades |
El doble de un número |
La cuarta parte de un número, menos su cuadrado | El precio de 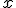 kg. de naranjas, si valen a 1,80 €/kg. kg. de naranjas, si valen a 1,80 €/kg. |
El 15% de un precio |
|
Expresión algebraica
(lenguaje matemático) |
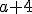 |
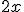 |
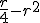 |
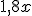 |
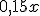 |
Valor numérico de una expresión algebraica
Una expresión algebraica también nos puede servir para buscar generalizaciones de un problema.
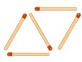
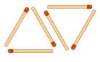
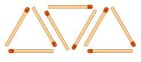
Imagina que construimos triángulos con cerillas del siguiente modo:
|
Nº de
triángulos (n) |
1 |
2 |
3 |
4 |
 |
 |
 |
 |
|
|
Nº de cerillas (p) |
3 |
6 |
9 |
12 |
¿Podríamos averiguar cuántas cerillas necesito si quiero formar 100 triángulos?
Para ello tenemos que encontrar una relación entre el número de triángulos (n) y el número de cerillas (p). Si te fijas, por cada triángulo necesito 3 cerillas, por lo que podríamos deducir que p=3n. Conociendo esta regla, ya puedo saber que para n=100 será p=3·100=300 cerillas.
Actividad
AV - Actividad de Espacios en Blanco
Ejemplo o ejercicio resuelto
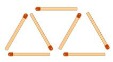
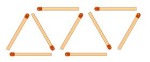
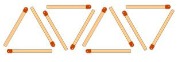
Vamos a buscar una fórmula que me diga el número de cerillas que necesito para formar los siguientes triángulos. Es parecido al ejemplo del apartado anterior, pero con una modificación: los triángulos se superponen.
|
Nº de
triángulos (n) |
1
|
2
|
3
|
4
|
|
Nº de cerillas (c) |
3 |
5 |
7 |
9 |
¿Cuál es la fórmula que relaciona el número de cerillas con el número de triángulos?