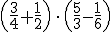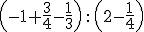4.1. Fracciones
 |
|
Imagen de Canislupusarctos en Wikimedia Commons. Licencia CC |
En la actualidad, se habla mucho del proceso de independencia de Cataluña, de cómo se fraccionaría España o de que solo una fracción de la población está a favor de dicho proceso. Precisamente, el concepto de fracción da nombre a un procedimiento basado en dividir (fraccionar) algo en partes.
En matemáticas, cuando queremos expresar una parte de un total recurrimos a los números fraccionarios o fracciones.
Los elementos que forman la fracción, y que se escriben separados por una raya horizontal, son:
- El denominador. Es el número de abajo, indica el número de partes iguales en que se divide la unidad.
- El numerador. Es el número de arriba, indica la cantidad de esas partes que se toman.
¿Cómo leemos las fracciones?
Primero se lee el numerador como cualquier número, y a continuación el denominador de la siguiente manera:
- Si es 2, 3, 4, 5, 6, 7, 8, 9 se lee: medios, tercios, cuartos, quintos, sextos, séptimos, octavos y novenos.
- Si es 10 se lee décimos; si es mayor que 10 se lee el número añadiendo la terminación -avos.
Así, un minuto es un sesentavo de hora y se representa por 
. Si tomamos cinco minutos, se lee como cinco sesentavos de hora, y se representa por 
.
Importante
Una fracción también puede entenderse como el cociente de dos números. Es decir, es una división sin realizar donde el numerador es el dividendo y el denominador el divisor.
Luego, para saber cuál es el valor de una fracción deberíamos realizar esa división. Sin embargo, con la simple observación del numerador y del denominador podemos hacernos una idea de ese valor:
- Si el numerador es más pequeño que el denominador, entonces la fracción vale menos de 1.
- Cuanto más cerca esté el numerador del denominador más cerca estará el valor de 1.
- Si el numerador es mayor que el denominador, entonces la fracción vale más de 1.
En general, su valor será más grande cuanto mayor tenga el numerador, y será más pequeño cuanto mayor tenga el denominador.
Comprueba lo aprendido
En el siguiente applet, prueba a ordenar las fracciones siguiendo las directrices anteriores:
Escena de Eduardo Barbero Corral en Proyecto Descartes. Licencia CC
Caso práctico
María se ha comido 3 partes de un bizcocho que se había dividido previamente en 8 partes iguales.
a) ¿Qué fracción representa lo que se ha comido María?
b) ¿Y la parte de bizcocho que ha sobrado?
c) Representa cada una de las fracciones anteriores mediante un dibujo.
Importante
Todo número que pueda ponerse en forma de fracción se dice que es un número racional.
Fracciones equivalentes. Operaciones con fracciones
Una de las peculiaridades que plantean las fracciones es que una misma medida (un mismo número) puede expresarse de formas distintas. Así, media hora 
puede expresarse también como 30 minutos, 
de hora, o como dos cuartos de hora, 
. Esto, en principio, puede considerarse un trastorno, pero precisamente esta propiedad es la que nos permite comparar, sumar y restar fracciones.
Importante
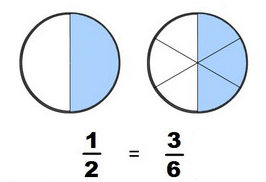
Llamamos fracciones equivalentes a aquellas que representan la misma cantidad. Para comprobar que dos fracciones son equivalentes multiplicamos en cruz el numerador de la primera por el denominador de la segunda y, si obtenemos el mismo resultado que al multiplicar el denominador de la primera por el numerador de la segunda, entonces las fracciones son equivalentes.
Para recordar cómo se operaba con fracciones te recomendamos que tengas a mano el siguiente pdf:
Pdf elaborado por Jesús Plaza M. en 3con14. Licencia CC
y que visualices la lista de reproducción compuesta por 10 vídeos en la que se da un repaso a todos los conceptos trabajados en el apartado Números racionales:
Lista de reproducción de Tuto mate alojado en Youtube
Ejercicio Resuelto
Resuelve las siguientes operaciones
Curiosidad
LEGO es una empresa y marca de juguetes danesa reconocida principalmente por sus bloques de plástico que se conectan entre sí y permiten hacer construcciones.
Dada su popularidad, su fácil manejo y su atractivo visual, se pueden utilizar para ejemplificar situaciones matemáticas, tal y como se recoge en este artículo que te enlazamos: Aprende Matemáticas con Lego. Concretando lo abstracto.
Te recomendamos el siguiente vídeo. Aunque las pocas palabras que aparecen están en inglés, solo la exposición te puede ayudar a comprender el concepto de fracciones equivalentes.
Vídeo de Kidspot alojado en Youtube