3.3. Divisibilidad. MCM y MCD

Frente a lo que pudiera parecer, la operación producto de números enteros ha tenido mayor importancia que la suma. El producto ha permitido un mayor conocimiento de los números enteros e interesantes aplicaciones prácticas. Por ejemplo, la clasificación de los números primos, que son esenciales en las labores de codificación en informática y en la creación de claves.

barbacoa

Imagen de moerschy en Pixabay. Licencia Pixabay

Importante

Si con y 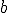números enteros distintos de 0, entonces

y 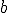se llaman divisores o factores de . También se dice múltiplo de y .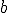

Dado que 2·5=10, 2 y 5 son divisores o factores de 10. A su vez, 10 es un múltiplo de 2 y de 5.
Decir que 2 es un divisor de 10 es equivalente a decir que 10 es un múltiplo de 2.

Por tanto, los múltiplos de un número natural son los números naturales que resultan de multiplicar ese número por otros números naturales:

Vídeo de lasmatematicas.es alojado en Youtube

Ser divisor es lo recíproco a ser múltiplo. Si 9 es múltiplo de 3, entonces 3 es divisor de 9. Los divisores de un número natural lo pueden dividir de forma exacta.

Para hacer más operativa la búsqueda de los divisores de un número, tenemos los criterios de divisibilidad.

Los criterios de divisibilidad son reglas que nos permiten averiguar con rapidez si un número es divisible por otro; es decir, si el más grande es múltiplo del más pequeño o si el más pequeño es divisor del más grande.

criterios de divisibilidad

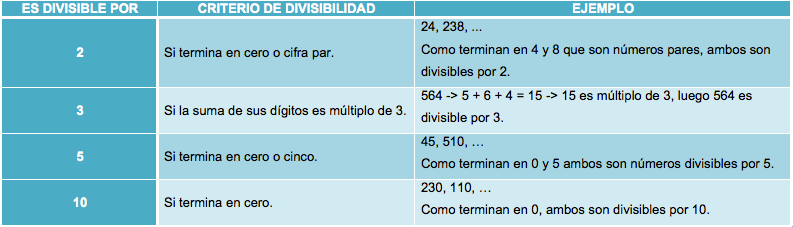
Estos criterios de divisibilidad no solo nos permiten reconocer, sin realizar la división, si un número es divisible por otro, sino también descomponer el número como un producto de otros números.

En la siguiente presentación descubrirás cómo se hace esta descomposición y cómo, a través de ella, podemos calcular el máximo común divisor y el mínimo común múltiplo, conceptos que te serán muy útiles de aquí en adelante.

Presentación de elaboración propia

Comprueba lo aprendido

A continuación, algunos ejercicios para practicar la descomposición en factores primos:

Escena de Eduardo Barbero Corral en Proyecto Descartes. Licencia CC

Caso práctico

En nuestro instituto funcionan cinco talleres: fotografía, ajedrez, canto, teatro y literatura. Las reuniones del taller de fotografía se hacen cada dos días, las del de ajedrez cada tres, las del de canto cada cuatro días, las del de teatro cada cinco días y las del de literatura cada seis días.

Si el día 1 de Octubre se reunieron los cinco talleres, ¿cuándo volverán a coincidir las reuniones de todos los talleres?

Retroalimentación

Observa que el número buscado debe ser múltiplo de los 5 números dados, ya que un taller se reúne cada vez que suma una cantidad fija de días, es decir, va construyendo un serie de múltiplos (p.e. ajedrez se reúne a los 3 días, a los 6 días, a los 9 días, ..., el de teatro a 5 días, a los 10, a los 15,...).

Por tanto, queremos un múltiplo común, y deseamos saber la primera vez que ocurrirá; luego, buscamos el MÍNIMO COMÚN MÚLTIPLO.

Como hemos visto antes, descomponemos todos los números en factores primos y tomamos los factores comunes y no comunes con mayor exponente. De ese modo, es múltiplo de todos y es el más pequeño posible.

Pues bien, haciendo eso obtenemos que 2,3 y 5 son números primos, 4 = 2² y 6 = 2·3; Por tanto el mínimo común múltiplo es 2²·3·5 o, lo que es lo mismo, 60.

Luego, vuelven a coincidir cada 60 días. Si coincidieron el día 1 de octubre, la próxima vez será el 30 de noviembre.

Curiosidad

Otras clasificaciones de números

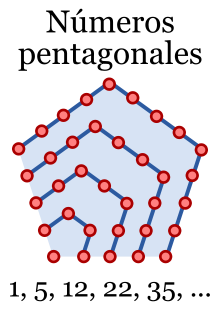
Los números poligonales los descubrieron los pitagóricos que utilizaban piedras o guijarros para formar figuras geométricas. Por ejemplo, tenemos números hexagonales y pentagonales:

Números hexagonales

1, 6, 15, 28, 45, ...

Imagen de Drini en Wikimedia Commons. Licencia CC

Imagen de Onmywaybackhome en Wikimedia Commons. Licencia Dominio Público

Un número perfecto es un número natural que es igual a la suma de los divisores propios positivos, sin incluirse él mismo. Por ejemplo, 6 es un número perfecto, pues si sumamos sus divisores propios no negativos y distintos de 6, es decir 1+2+3, el resultado es 6.

Números amigos. Dos números son amigos si la suma de los divisores propios de uno da como resultado el otro, y viceversa. Por ejemplo, 220 y 284 son amigos.

Números primos gemelos. Son parejas de números primos que están separados por una distancia de 2. Pero mejor te lo explica Jeff Bridges:

Vídeo de Pilar Gallego alojado en Youtube