3.2. Operaciones
Suma y resta de números enteros
Aunque el valor absoluto y el opuesto también son operaciones, este apartado lo dedicaremos a las operaciones "clásicas" (por clásicas no nos referimos a más antiguas, pero sí seguro que a las que más recuerdas).
Reflexión
Manipula el siguiente applet de Geogebra y plantéate las siguientes preguntas:
- ¿Qué ocurre si a y b tienen el mismo signo?
- ¿Y si tienen signo contrario?
Importante
En el caso de la suma de dos números enteros distinguimos dos casos:
- Que ambos números tengan el mismo signo. En este caso, el signo del resultado es el signo común de los sumandos. El valor absoluto del resultado es la suma de los valores absolutos de los sumandos.
- Que los números a sumar tengan distinto signo. En este caso el resultado adopta el signo del sumando de mayor valor absoluto. El valor absoluto del resultado es la diferencia entre el mayor valor absoluto de los sumandos y el menor.
La operación resta o diferencia entre números enteros se puede entender como un caso particular de la suma: a - b = a + (-b), donde a y b son números enteros.
En el siguiente vídeo puedes ver estas definiciones con ejemplos:
Vídeo de Tuto mate alojado en Youtube
Importante
Nunca pueden aparecer dos signos (operaciones) seguidos. Tienen que estar separados por paréntesis, corchetes...
Multiplicación y división
Sabemos que multiplicar consiste en sumar un número (multiplicando) tantas veces como indica otro número (multiplicador), y que en el caso de que sea posible efectuar la división, esta consiste en indagar cuántas veces un número (divisor) está "contenido" en otro número (dividendo). La operación división entre números enteros no siempre da como resultado un número entero (pasa algo parecido a lo que ocurría con la resta de números naturales).

Importante
El producto (o, análogamente, división) de dos números enteros se obtiene ateniéndose a las reglas:
- El valor absoluto del resultado es el producto (o la división) de los valores absolutos.
- El signo se obtiene mediante la regla del producto (o la división) de los signos:
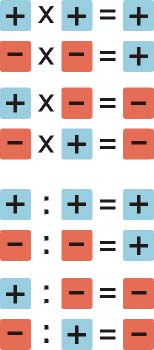
Imagen de Antonio Ortega Moreno alojada en Intef. Licencica CC
Las operaciones con números enteros cumplen las mismas reglas que las operaciones con números naturales.
Ejercicio Resuelto
Realiza las siguientes operaciones combinadas de números enteros:
-
- -3·[(2 - 1 - 7) - 8]
- 2·(-8 - 4 + 12) - 3·[7 - (-2 + 1)]
En el siguiente vídeo podemos ver cómo operar combinando estas operaciones
Potencias
Al igual que la multiplicación es la suma de un mismo número varias veces, la potenciación es el producto resultante de multiplicar una o varias veces ese número.
Las potencias se representan 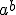 donde
donde  es el número que se multiplica (base) y
es el número que se multiplica (base) y 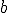 el número de veces que se hace el producto (exponente).
el número de veces que se hace el producto (exponente).
Así, por ejemplo, 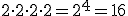 .
.
Sus propiedades son muy prácticas a la hora de simplificar cálculos:
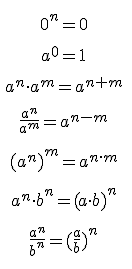
Ejercicio Resuelto
Calcula las siguientes potencias
a) 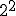 b)
b) 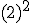 c)
c) 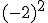 d)
d)  e)
e) 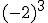 f)
f) 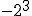
Ejercicio Resuelto
Resuelve las siguientes potencias:
a) 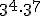 b)
b) 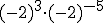 c)
c) 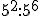 d)
d) 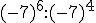 e)
e) 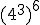
f) 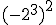 g)
g)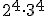 h)
h) 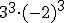 i)
i) 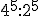 j)
j) 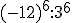
Importante
Si observas detenidamente el ejemplo anterior, podrás sacar algunas conclusiones:
- Si el signo está dentro del paréntesis, formará parte de la base y, por consiguiente, se repetirá tantas veces como nos indica el exponente.
- Si el signo está fuera del paréntesis, no forma parte de la base y, por consiguiente, se añadirá al resultado de la potencia.
- Si la base es positiva, el resultado será positivo.
- Si la base es negativa y el exponente es par, el resultado será positivo.
- Si la base es negativa y el exponente es impar, el resultado será negativo.
Estamos en números enteros, hemos hablado de potencias con base positiva y negativa, y exponentes positivos. Pero... ¿qué ocurre con los exponentes negativos? ¿No existen potencias con exponentes negativos? La respuesta es sí, pero tendrás que descubrirlas en el apartado cuarto.