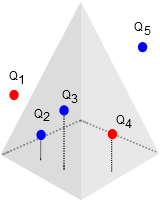
2. Teorema de Gauss

Imagen en Wikimedia Commons, de Gottlieb Biermann A. Wittmann (foto) bajo dominio público

Nuestro amigo Gauss (Carl Friedrich Gauss), es considerado "el príncipe de los matemáticos", el matemático más grande desde la antigüedad.

Entre sus muchas contribuciones a la Matemática, a la Física le interesan, en particular, sus estudios sobre los campos vectoriales. Uno de los resultados de ese estudio se plasma en el teorema de la divergencia, cuya aplicación a la teoría de campos es lo que solemos conocer como teorema de Gauss.

Aplicado al campo eléctrico, el teorema de Gauss relaciona el flujo de campo eléctrico a través de una superficie cerrada, con la carga neta encerrada por dicha superficie. El teorema dice así...

El flujo de campo eléctrico a través de una superficie cerrada es proporcional a la carga neta encerrada por la misma

Expresión en la que, por sencillez, se supone que el sistema se encuentra en el vacío () y donde  representa a la carga neta encerrada por la superficie cerrada S.

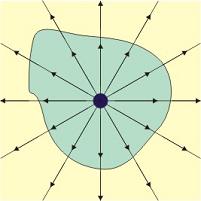
Es un teorema fácil de comprender, como verás si prestas atención a las siguientes imágenes. En ellas se muestra una carga puntual y el campo eléctrico creado por ella, junto con una superficie cerrada (bueno, en realidad, un corte de una superficie cerrada:

Ilustración en Wikimedia Commons de Gonfer, bajo CC	Ilustración en Wikimedia Commons de Gonfer, bajo CC
En la imagen de arriba , puedes ver que la carga puntual está situada en el interior de la superficie. Todas las líneas de campo atraviesan la superficie en el mismo sentido, hacia afuera. Hay un flujo de campo positivo a través de la superficie cerrada.	En la imagen superior, la carga puntual está fuera de la superficie. En esta ocasión, todas las líneas de campo que entran en la superficie cerrada... vuelven a salir de ella. El flujo de campo a través de la superficie cerrada es nulo.

Antes de pasar a los siguientes apartados, en los que vas a ver para qué nos sirve el teorema de Gauss, te recomiendo que veas este vídeo. Te servirá para repasar y afianzar lo que has aprendido sobre el teorema de Gauss.