3.1. Triángulo de Tartaglia
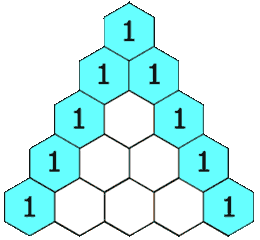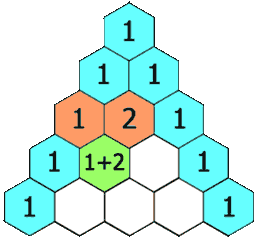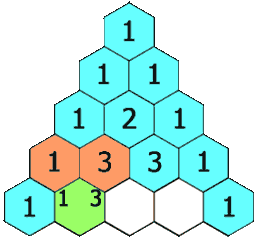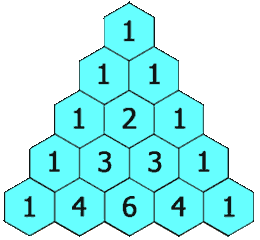
El triángulo de Tartaglia, auque también llamado triángulo de Pascal, es un triángulo formado por números combinatorios. El procedimiento para construir dicho triángulo es sumamente sencillo, comenzamos fabricando el vértice con el número ![]() . La segunda fila, la construimos añadiendo en una fila inferior los números
. La segunda fila, la construimos añadiendo en una fila inferior los números ![]() obteniendo la siguiente triángulo.
obteniendo la siguiente triángulo.
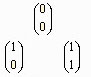
Añadimos ahora nueva nueva fila, con los valores 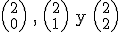 , obteniendo un paso mas del triángulo de Tartaglia. Si realizamos varios pasos mas llegamos al siguiente
, obteniendo un paso mas del triángulo de Tartaglia. Si realizamos varios pasos mas llegamos al siguiente
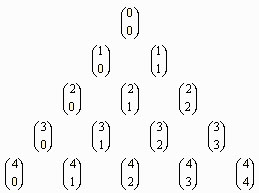
Si calculamos el valor de los números combinatorios, llegamos al siguiente triángulo.

Pregunta de Elección Múltiple
Actividad
El triángulo de Tartaglia cumple una serie de propiedades:
- Si observamos cada fila, los valores en posiciones equidistantes de los extremos son iguales.
- La primera y última posición de cada fila, toma el valor 1.
- Para obtener un valor de cada fila, salvo el primero y el último, tan solo tenemos que sumar los dos términos que tiene sobre él en el triángulo.
- Si sumamos los terminos de la fila n, obtenemos 2n, tomando la primera fila, como la fila 0.
En esta animación se puede observar cómo se aplica la propiedad tres para generar nuevas filas del triángulo de Tartaglia de un modo fácil y cómodo.
|
Imagen en Wikimedia Commons |