2.1. Definición y propiedades
Actividad
El factorial de un número entero positivo n, denotado por n!, es el resueltado de multiplicar el todos los números enteros positivos desde 1 hasta el propio número, es decir:
n! = n·(n-1)·(n-2)·...·3·2·1
Aquí puedes ver una tabla con los factoriales de los 13 primeros números naturales. Fíjate con la velocidad que crecen estos números.
| Número | Factorial |
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 479001600 |
Aquí tienes un enlace a la caluladora CALCME donde puedes calcular el factorial de cualquier número. Tan solo tienes que escribir el número al que quieras calularle el factorial y el símbolo !. Tras esto, pulsa el botón = que aparece en la página. Ten cuidado con números muy grandes, ya que es bastante costoso de calcular para el ordenador.
Actividad
Propiedades
-
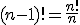
- Si m>n entonces
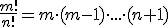
Una propiedad muy importante a la hora de trabajar con números factoriales es la siguiente 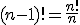 . Como puedes comprobar, su deducción es inmediata a partir de la definición que hemos visto
. Como puedes comprobar, su deducción es inmediata a partir de la definición que hemos visto
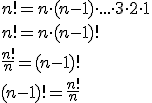
Te hacemos ahora una de esas preguntas que, a priori, no tienen respuestas ¿cual es el valor de 0!? ¿Como podemos utilizar la definición de número factorial para calular 0!?
Actividad
Si utilizamos la anterior propiedad para n = 1, obtenemos inmediatamente el valor de 0!
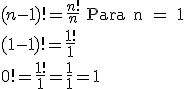
Por lo tanto 0! = 1
Reflexión
Pregunta de Elección Múltiple
Pregunta Verdadero-Falso
Retroalimentación
Falso
Con 6 números distintos podemos formar exactamente 6! números, es decir, 720. Por la tanto la afirmación es falsa.